ilya
- 3
- 0
Please help. I am starting to think the answer in the back of my book is wrong. Refer to picture below. Question: Find the speed of the elevator if the winches A and B both pull the rope at 5 m/s. Answer is 2.14m/s. How? I have no idea. I am not the kind to just give up.
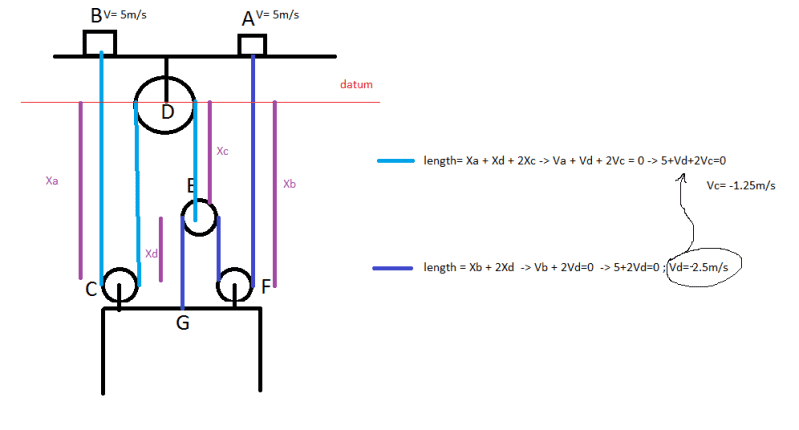
Thank you very much!
Thank you very much!