epheterson
- 22
- 0
Homework Statement
Includes picture, download question http://docs.google.com/Doc?id=ajccwmhrc3rx_37gs2ht7g9" .
Homework Equations
The potential energy equation ends up being
V = 1/2 k x^2 + W y
The Attempt at a Solution
xspring = 2 sin(\Theta)
ym = 2 cos(\Theta)
V = 1/2*40 (2 * sin(\Theta))^2 + 7 * 2 * g cos \Theta
dV/d\Theta = 160sin(\Theta)cos(\Theta)-14g*sin(\Theta) = 0
Solving returns theta = 0, 0.5404057 rad (31 degrees)
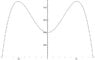
That sounds about right, so now I look for stability
d^2V/d\Theta^2 = 160cos(\Theta)^2-160sin(\Theta)^2-14g*cos(\Theta)
This is where I'm stuck. Using intuition, I feel the system should be UNstable at theta = 0 and find stability at theta = 31 degrees.
Solving the second derivative, I get d^2V/d\Theta^2(0) > 0 and d^2V/d\Theta^2(.54) < 0
Is the math wrong or is my understanding of stability wrong?
Last edited by a moderator: