novafx
- 7
- 0
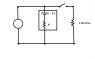
This is just a general question that will help me start a problem, so I have no work to show. The question is: How can you tell that a problem is a multiloop circuit? Does it correspond to the number of voltage sources (batteries) in the circuit, or is it based off of how the components of the circuit are arranged? If it's the second one, could you tell me how to tell where the components would typically be for a multiloop circuit? I guess that's more than one question.  Thanks for the help!
Thanks for the help!