How to find forces in wires at equilibrium

[harmyder]

I need to find tensions in suspensions wires on the picture:

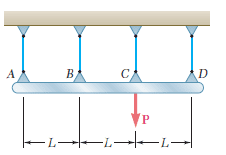
I wrote 4 equilibrium equations for moments in A, B, C, D and equilibrium about y-axis, but i got matrix with rank two.

$$\begin{pmatrix}<br /> 3 & 2 & 1 & 0 \\<br /> 0 & 1 & 2 & 3 \\<br /> -1 & 0 & 1 & 2 \\<br /> -2 & -1 & 0 & 1 \\<br /> 1 & 1 & 1 & 1<br /> \end{pmatrix}<br /> \begin{pmatrix}<br /> F_A \\<br /> F_B \\<br /> F_C \\<br /> F_D<br /> \end{pmatrix}<br /> =<br /> \begin{pmatrix}<br /> 1 \\<br /> 2 \\<br /> 1 \\<br /> 0 \\<br /> 1<br /> \end{pmatrix}$$

How to find the forces?

 

[haruspex]

Yes, there ard only two equations to be had from the usual linear and rotational force balances. To get further, you will need to make assumptions about how the wires and beam deform under loads.

 

[haruspex]

Yes, there ard only two equations to be had from the usual linear and rotational force balances. To get further, you will need to make assumptions about how the wires and beam deform under loads.

... Specifically, I would suggest taking the beam to be completely straight and rigid, but allow the wires all the same modulus of elasticity. That is enough to get a solution.

 

[harmyder]

$$\delta_A = \delta_C - 2x$$$$\delta_B = \delta_C - x$$$$\delta_D = \delta_C + x$$
Thus,
$$F_A = \frac{\delta_A SE}{L} = \frac{\delta_C SE}{L} - 2x\frac{SE}{L}$$

And further,
$$F_B - F_A = F_C - F_B = F_D - F_C.$$

Now matrix looks like this:
$$\begin{pmatrix}<br /> -1 & 2 & -1 & 0 \\<br /> 0 & -1 & 2 & -1 \\<br /> 3 & 2 & 1 & 0 \\<br /> -1 & 0 & 1 & 2<br /> \end{pmatrix}<br /> \begin{pmatrix}<br /> F_A \\<br /> F_B \\<br /> F_C \\<br /> F_D<br /> \end{pmatrix}<br /> =<br /> \begin{pmatrix}<br /> 0 \\<br /> 0 \\<br /> 1 \\<br /> 1<br /> \end{pmatrix}$$

It has solution 0.1, 0.2, 0.3, 0.4.

 

[haruspex]

$$\delta_A = \delta_C - 2x$$
$$\delta_B = \delta_C - x$$
$$\delta_D = \delta_C + x$$
Thus,
$$F_A = \frac{\delta_A SE}{L} = \frac{\delta_C SE}{L} - 2x\frac{SE}{L}$$

And further,
$$F_B - F_A = F_C - F_B = F_D - F_C.$$

Now matrix looks like this:
$$\begin{pmatrix}<br /> -1 & 2 & -1 & 0 \\<br /> 0 & -1 & 2 & -1 \\<br /> 3 & 2 & 1 & 0 \\<br /> -1 & 0 & 1 & 2<br /> \end{pmatrix}<br /> \begin{pmatrix}<br /> F_A \\<br /> F_B \\<br /> F_C \\<br /> F_D<br /> \end{pmatrix}<br /> =<br /> \begin{pmatrix}<br /> 0 \\<br /> 0 \\<br /> 1 \\<br /> 1<br /> \end{pmatrix}$$

It has solution 0.1, 0.2, 0.3, 0.4.

That's the answer I get.