How to find the angle of a pinned rod at a certain depth

[hdp12]

Homework Statement

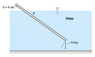
The uniform 5 m-long round wooden rod (ρ = 800 kg/m3 ) is tied to the bottom by a string with length 1 m. Determine the inclination angle θ if the water level is 3.5 m. What if the water level is 7m?

Homework Equations

Fb = ρgV

The Attempt at a Solution

So I'm really struggling with the conceptualization of this one.
I know that
Fg on rod = ρ_rod⋅V_rod⋅g
FB = ρ_water⋅V_displaced⋅g

if the depth of the water is 1 m, then there is no y-force on the string. This means that at a water depth of 1 m, the gravitational force is equal to the buoyancy force.
This means that the volume of water displaced is...
( I calculated it out )... 0.02011 m³

What, however, must I do when I begin to increase the water level?

 

[BvU]

Nice exercise ! You know how much of the stick is above water as a function of $\theta$, right ? The make a free body diagram (a force balance).