Tater
- 9
- 0
Hi everyone,
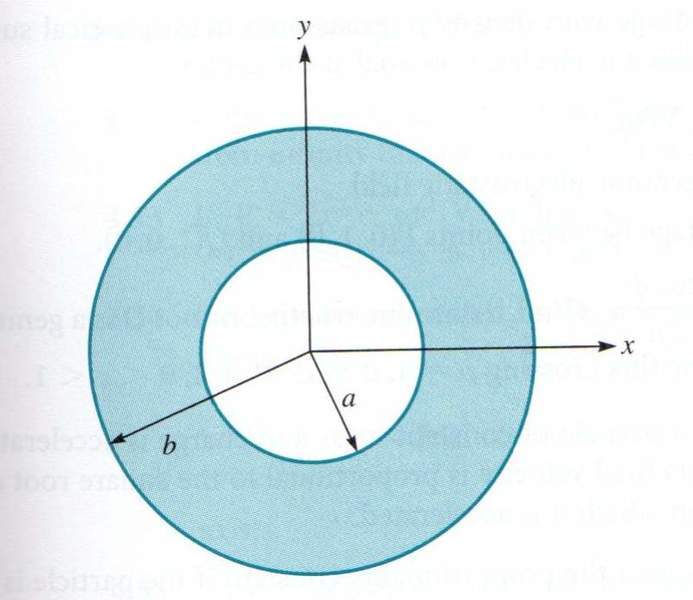
Let a charge Q be uniformly distributed on a circular ring defined by a < \rho < b. Find D at (0,0,h).
E = kQ/r2 ar
D = \epsilono E
Well I thought I had this figured out, but I was wrong and I still can't figure it out after 2 hours :(
Since I have a range for the radius (a and b), I thought that I could calculate the E-field for both a and b separately then simply apply b-a to the field.
Finding both r1 and r2:
cos ∅1 = h / r1 = h / \sqrt{a^2 + h^2}
cos ∅2 = h / r2 = h / \sqrt{b^2 + h^2}
Then, E = kQh / r^2 [ cos ∅1 - cos ∅2 ]
I just don't know how to tackle this one. I have a large gap that I need to make note of.
The solution in the back of the book is D = \frac{Qh}{2\pi(b^2-a^2)} [\frac{1}{\sqrt{a^2+h^2}} - \frac{1}{\sqrt{b^2+h^2}} ]
I would greatly appreciate any help! I kind of think I had the right idea, I just don't understand how to fix what I've done wrong.
Any help is greatly appreciated! :)
Homework Statement
Let a charge Q be uniformly distributed on a circular ring defined by a < \rho < b. Find D at (0,0,h).
Homework Equations
E = kQ/r2 ar
D = \epsilono E
The Attempt at a Solution
Well I thought I had this figured out, but I was wrong and I still can't figure it out after 2 hours :(
Since I have a range for the radius (a and b), I thought that I could calculate the E-field for both a and b separately then simply apply b-a to the field.
Finding both r1 and r2:
cos ∅1 = h / r1 = h / \sqrt{a^2 + h^2}
cos ∅2 = h / r2 = h / \sqrt{b^2 + h^2}
Then, E = kQh / r^2 [ cos ∅1 - cos ∅2 ]
I just don't know how to tackle this one. I have a large gap that I need to make note of.
The solution in the back of the book is D = \frac{Qh}{2\pi(b^2-a^2)} [\frac{1}{\sqrt{a^2+h^2}} - \frac{1}{\sqrt{b^2+h^2}} ]
I would greatly appreciate any help! I kind of think I had the right idea, I just don't understand how to fix what I've done wrong.
Any help is greatly appreciated! :)