Electric field at the edge of half planes

[Bling Fizikst]

Homework Statement

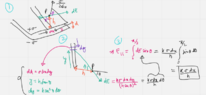
Two parallel half planes are uniformly charged with surface charge densities $+\sigma$ and $-\sigma$ . Find magnitude and direction of electric field due to point $P$ located at a height $h$ above the edge of the positively charged half-plane . Distance $d$ between the planes is much smaller than $h$ .

Relevant Equations

refer to the image

I assumed the plate areas to be $S$ , then electric field at $P$ should be $$E_P=E_{+\sigma}-E_{-\sigma}=\frac{k\sigma S}{h^2}-\frac{k\sigma S}{(h+d)^2}\approx \frac{2k\sigma S d}{h^3}$$ but i think it's wrong here as $P$ lies at the edge , so it won't recieve electric fields in a way which would satisfy the aforesaid equations . Morever , the area is unknown and i doubt that it could be found .

 

[Gordianus]

From your post I conclude you assumed the planes perform like point charges. I think it's wrong

 

[Bling Fizikst]

From your post I conclude you assumed the planes perform like point charges. I think it's wrong

Actually i was kinda motivated by Krotov problem $3.12$ . And thought it would work here as well . In that problem , we were asked to find force of interaction but as i had suspected the issue is due to the location of the field that we needed to take into account . Here we need to find the field at the edge while for the Krotov one , we need it at the center .

 

[Bling Fizikst]

Any elaborate ideas how to move forward? I tried to integrate strips , don't think that works either.

 

[Gordianus]

I don't have Krotov's book but I'm sure problem 3.12 is an example of the method of images. Your case Is different and requieres integration.

 

[TSny]

You can determine the vertical component of the net field at P without any integration if you are familiar with the well-known result for the field due to a uniformly charged infinite sheet. Think of an infinite sheet as the superposition of two semi-infinite sheets.

You can use integration of strips to find the horizontal component of the net field at P. The integration diverges for each sheet individually. But, if you set up one integral for both sheets together, the integral will converge. You can simplify the integrand by approximating it to first order in $d/h$ under the assumption that $d << h$.

 

[Bling Fizikst]

I am working on it . Can you confirm that the vertical component by gauss law is the usual $\frac{\sigma}{2\epsilon_{\circ}}$ by the positive plate and that should be the only component working because in between the plates , it is basically a capacitor and so it shouldnt affect the field at $P$ . \\\\ Also , i am getting the field due to the positive plate a converging integral , not sure how to take them together as you mention . I have provided my working as of now , sorry for it being messy . So , i marked them 1 ,2,3 in order . Btw there is a minor error in the work , it should be $dq=\sigma dx dy$ instead of $dA$ .

 

[Gordianus]

From your drawing I see that y/h=tan(theta) thus y=h tan(theta)

 

[TSny]

I am working on it . Can you confirm that the vertical component by gauss law is the usual $\frac{\sigma}{2\epsilon_{\circ}}$ by the positive plate

The vertical component of the field at P due to one of the semi-infinite sheets will not be the same as for an infinite sheet. But there is a simple relation between the vertical component at P due to the semi-infinite sheet and the vertical component due to an infinite sheet.

and that should be the only component working because in between the plates , it is basically a capacitor and so it shouldnt affect the field at $P$ .

I don't follow this.

Also , i am getting the field due to the positive plate a converging integral , not sure how to take them together as you mention . I have provided my working as of now , sorry for it being messy . So , i marked them 1 ,2,3 in order . Btw there is a minor error in the work , it should be $dq=\sigma dx dy$ instead of $dA$ .

If you orient the strips as you have, the point P will not be vertically above the end of a typical strip. So, the geometry and trig that you used will not apply to the typical strip. I recommend that you orient the strips as shown:

The strip is an infinite, uniformly charged line. The field at P due to the strip is easy to find using Gauss' law, or you might already be familiar with the field of an infinite line.

 

[Bling Fizikst]

Ohhk for the vertical component , i can imagine joining two semi infinite sheets together each with electric field $E$ to give a net field of an infinite sheet that is $\frac{\sigma}{2\epsilon_{\circ}}$ yielding $E=\frac{\sigma}{4\epsilon_{\circ}}$ Also , for field at $P$ , how do we find the area of the strip ? i know that for an infinite line with linear charge density $\lambda$ is $\frac{\lambda}{2\pi\epsilon_{\circ} r}$ at some radial distance $r$ . But in this case we have surface charge density .

 

[Gordianus]

The OP says we have half planes and that P lies at the edge of the half plane. We can't use results valid for an infinite distribution.

 

[TSny]

Ohhk for the vertical component , i can imagine joining two semi infinite sheets together each with electric field $E$ to give a net field of an infinite sheet that is $\frac{\sigma}{2\epsilon_{\circ}}$ yielding $E=\frac{\sigma}{4\epsilon_{\circ}}$

Ok. This argument applies only to the vertical component (call it$E_z$), of the field at P. The two semi-infinite sheets (that make up a full infinite sheet) each produce the same vertical component of field at P. [Edit: the vertical components of $\vec E$ at P from the two sheets have the same magnitude but opposite directions.]

Also , for field at $P$ , how do we find the area of the strip ? i know that for an infinite line with linear charge density $\lambda$ is $\frac{\lambda}{2\pi\epsilon_{\circ} r}$ at some radial distance $r$ . But in this case we have surface charge density .

The strip has an infintesimal width $dx$ (assuming the $x$-axis is oriented in the plane of the sheet and perpendicular to the edge of the semi-infinite sheet). Can you see how $\sigma$, $\lambda$, and $dx$ are related?

 

[TSny]

The OP says we have half planes and that P lies at the edge of the half plane. We can't use results valid for an infinite distribution.

We can relate the vertical component of the field at P due to the half plane to the field at P due to a full plane.

 

[Bling Fizikst]

Ok. This argument applies only to the vertical component (call it$E_z$), of the field at P. The two semi-infinite sheets (that make up a full infinite sheet) each produce the same vertical component of field at P.


The strip has an infintesimal width $dx$ (assuming the $x$-axis is oriented in the plane of the sheet and perpendicular to the edge of the semi-infinite sheet). Can you see how $\sigma$, $\lambda$, and $dx$ are related?

$\sigma dA=\lambda dx$ but we dont know $dA$ or $\lambda$ here?

 

[TSny]

$\sigma dA=\lambda dx$ but we dont know $dA$ or $\lambda$ here?

Ok. I was choosing the x-direction as perpendicular to the strip, while you are choosing the x-direction along the length of the strip. Let's go with your choice. Then, the y-axis will be perpendicular to the strip and the width of the strip will be $dy$. Note that if we choose a small length $dx$ of the strip of width $dy$, then $dA = dx dy$. Substitute this expression for $dA$ into your equation $\sigma dA = \lambda dx$ and simplify.

 

[Bling Fizikst]

Well , simplifying gives me $\lambda=\sigma dy\implies E=\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{h^2+y^2}}$ so this is the radial field due to the positive half plane plane . Similarly for the negative half plane , it is $\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{y^2+(h+d)^2}}$ . It seems a bit weird , not sure what to do next .

 

[Gordianus]

The electric field at P must be a vector. Post #16 gives the (wrong) modulus of the electric field at P as a function of the distance "y" along the plane.

 

[TSny]

Well , simplifying gives me $\lambda=\sigma dy\implies E=\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{h^2+y^2}}$
so this is the radial field due to the positive half plane plane .

$\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{h^2+y^2}}$ is the radial field $dE$ due to the strip of width $dy$ located at $y$ in the positive half plane.

Which component of $dE$ do you think you should be working with at this point?

How would you set up an integral to evaluate this component of the total field at P due to all of the strips making up the positive half-plane?

Similarly for the negative half plane , it is $\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{y^2+(h+d)^2}}$ .

Ok, this looks good for the magnitude of $dE$ for a strip in the negative half-plane

 

[TSny]

The electric field at P must be a vector. Post #16 gives the (wrong) modulus of the electric field at P as a function of the distance "y" along the plane.

The expression in #16 looks correct to me for the magnitude of the electric field $dE$ at P due to the strip at $y$.

 

[Bling Fizikst]

$\frac{\sigma dy}{2\pi\epsilon_{\circ}\sqrt{h^2+y^2}}$ is the radial field $dE$ due to the strip of width $dy$ located at $y$ in the positive half plane.

Which component of $dE$ do you think you should be working with at this point?

How would you set up an integral to evaluate this component of the total field at P due to all of the strips making up the positive half-plane?


Ok, this looks good for the magnitude of $dE$ for a strip in the negative half-plane

If i think straight , it should be $E=\int \left(dE_{+\sigma}-dE_{-\sigma}\right)=\int_{0}^{\infty}\frac{\sigma}{2\pi\epsilon_{\circ}}\left[\frac{1}{\sqrt{y^2+h^2}}-\frac{1}{\sqrt{y^2+(h+d)^2}}\right]\cdot dy$ $$E=\frac{\sigma}{2\pi\epsilon_{\circ}}\left[\ln\left(\frac{y+\sqrt{y^2+h^2}}{y+\sqrt{y^2+(h+d)^2}}\right)\right]_{0}^{\infty}$$ $$\implies \lim_{y\to\infty} \ln\left(\frac{y+\sqrt{y^2+h^2}}{y+\sqrt{y^2+(h+d)^2}}\right) = \ln(1)=0$$ $$\lim_{y\to 0} \ln\left(\frac{y+\sqrt{y^2+h^2}}{y+\sqrt{y^2+(h+d)^2}}\right)=\ln\left(\frac{h}{h+d}\right)=- \ln\left(1+\frac{d}{h}\right)=-\frac{d}{h}$$ Substituting them and subtracting to get $$E=\frac{\sigma}{2\pi\epsilon_{\circ}}\left[0-\left(\frac{-d}{h}\right)\right]$$ $$E=\frac{\sigma d}{2\pi\epsilon_{\circ}h}$$

 

[TSny]

If i think straight , it should be $E=\int \left(dE_{+\sigma}-dE_{-\sigma}\right)=\int_{0}^{\infty}\frac{\sigma}{2\pi\epsilon_{\circ}}\left[\frac{1}{\sqrt{y^2+h^2}}-\frac{1}{\sqrt{y^2+(h+d)^2}}\right]\cdot dy$

As pointed out by @Gordianus in post #17, each infinitesimal strip produces an electric field vector $d\vec {E}$ at point P. The total field at P is the vector sum of the fields $d\vec {E}$ due to all the strips. Since $d\vec{E}$ from different strips have different directions at P, you need to work with components. See the figure in post #19.

 

[Bling Fizikst]

As pointed out by @Gordianus in post #17, each infinitesimal strip produces an electric field vector $d\vec {E}$ at point P. The total field at P is the vector sum of the fields $d\vec {E}$ due to all the strips. Since $d\vec{E}$ from different strips have different directions at P, you need to work with components. See the figure in post #19.

As evident from the attached figure , $$dE_y=dE_{+\sigma}\sin\alpha-dE_{-\sigma}\sin\beta$$ $$dE_z=dE_{+\sigma}\cos\alpha-dE_{-\sigma}\cos\beta$$On doing the integration we get : $$E_y = \frac{\sigma d}{2\pi\epsilon_{\circ} h}$$ $$E_z=0$$ Hence , $$\boxed{\vec{E}=\frac{\sigma d}{2\pi\epsilon_{\circ} h} \hat{j}}$$

 

[TSny]

As evident from the attached figure , $$dE_y=dE_{+\sigma}\sin\alpha-dE_{-\sigma}\sin\beta$$ $$dE_z=dE_{+\sigma}\cos\alpha-dE_{-\sigma}\cos\beta$$On doing the integration we get : $$E_y = \frac{\sigma d}{2\pi\epsilon_{\circ} h}$$ $$E_z=0$$ Hence , $$\boxed{\vec{E}=\frac{\sigma d}{2\pi\epsilon_{\circ} h} \hat{j}}$$

Ok. I believe those answers are correct.

It's nice to see that the integration for $E_z$ gives zero in agreement with post #10 where you had $E_z = \frac {\sigma}{4 \epsilon_0}$ for one sheet. So, the two oppositely charged sheets together give $E_z = 0$.

 

[Bling Fizikst]

Ok. I believe those answers are correct.

It's nice to see that the integration for $E_z$ gives zero in agreement with post #10 where you had $E_z = \frac {\sigma}{4 \epsilon_0}$ for one sheet. So, the two oppositely charged sheets together give $E_z = 0$.

Thank you for helping me out!