SUMMARY
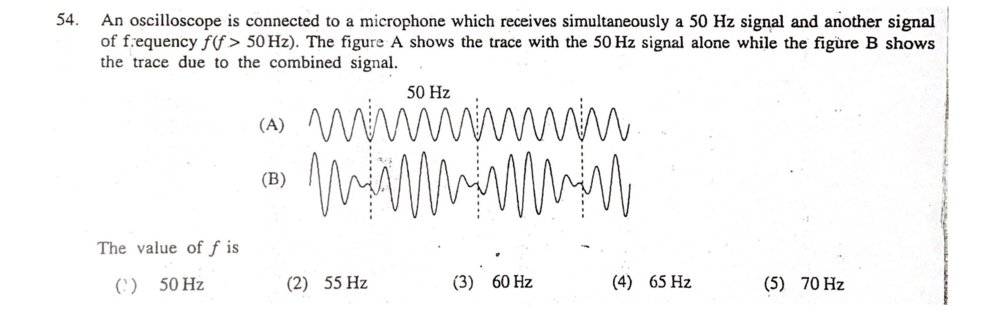
The discussion centers on determining the frequency of a second wave (signal C) using the concept of beat frequency. The beat frequency is defined as the difference between the frequencies of two waves, specifically frequency of wave 2 (signal C) and frequency of wave 1 (signal A). The participants conclude that if signal A has a frequency of 50Hz and the beat frequency is 10Hz, then signal C must be 60Hz. This conclusion is reached by analyzing the waveforms and applying the beat frequency equation.
PREREQUISITES
- Understanding of beat frequency in wave physics
- Knowledge of waveform analysis
- Familiarity with frequency calculations
- Basic principles of wave interference
NEXT STEPS
- Study the concept of beat frequency in wave mechanics
- Learn how to analyze waveforms for frequency determination
- Explore the mathematical relationships between wave frequencies
- Investigate real-world applications of beat frequency in acoustics
USEFUL FOR
Students and professionals in physics, audio engineering, and anyone interested in wave phenomena and frequency analysis.