How to find the same angle in different orientations?

[eggshell]

Homework Statement

This is from a homework that's already been graded, and this is the solution:

http://desmond.imageshack.us/Himg842/scaled.php?server=842&filename=angler.jpg&res=medium

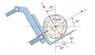
I just want to know the reasoning behind the placement of the the 30 degree angles in the free body diagram given only the original picture.

The Attempt at a Solution

The only reasoning that I can see is that if you readjusted the axis to it's more typical x and y directions, then the force resulting from gravity acting on the object would overlap the -x axis. So by tilting the coordinate axis 30 degrees, a 30 degree angle forms between the G force and the NB force, because the G force always points directly down. Is there a better proof for this? Am I wrong in my reasoning for the placement of that angle? If it is relevant, this is for a statics class.

 

[gneill]

The coordinate axes are chosen, for expediency, so as to coincide with the normal forces at points A and B. It just so happens that the L-shaped bracket is tilted by 30° from the horizontal.

 

[eggshell]

I know why the coordinate axes are tilted in the way that they are, but my question is how does one recognize that the 30 degree angle (in the free body diagram) is the same angle as the one shown in the picture.

 

[gneill]

I know why the coordinate axes are tilted in the way that they are, but my question is how does one recognize that the 30 degree angle (in the free body diagram) is the same angle as the one shown in the picture.

The coordinate system is rotated by 30°. The direction of "down", in which the gravitational force is directed, remains unchanged, so the coordinate system is rotated with respect to this direction.