lachgar
- 6
- 0
- Homework Statement
- An elastic homogene and isotrope cuboid that is under a constant pressure (-p) in its 4 lateral surfaces. We neglect the weight .
- Relevant Equations
- equilibre equation, bondary conditions, s
Good evening everybody.
This is my suggestion for answer.
The tensor is diagonal and the compression is a plane stress
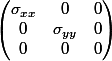
equilibre equation div(σ)=0
so:
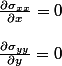
So, does that means that
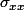 = f(y.z) = Ay+Bz and
= f(y.z) = Ay+Bz and
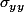 =f(x.z)= Cx+Dz
=f(x.z)= Cx+Dz
A,B,C and D are constants.
Is that what the question meant?
Thank you in advance.
This is my suggestion for answer.
The tensor is diagonal and the compression is a plane stress
equilibre equation div(σ)=0
so:
So, does that means that
A,B,C and D are constants.
Is that what the question meant?
Thank you in advance.