How to Graph Potential Energy from Force Fx Along the x-axis?

[bestchemist]

1. Homework Statement

The figure shows the force Fx exerted on a particle that moves along the x-axis. Draw a graph of the particle's potential energy as a function of position x from 0m to 1.1m. Let U be zero at x=0m.

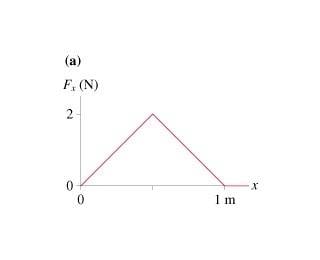
2. Homework Equations

W = F*d
U = mgh

 

[PhanthomJay]

Attempt please. Your relevant equations are not correct when the force is not constant. The force is not mg. Are you familiar with calculus or other means of calculating work or PE for non constant (assumed conservative) forces?

 

[bestchemist]

Attempt please. Your relevant equations are not correct when the force is not constant. The force is not mg. Are you familiar with calculus or other means of calculating work or PE for non constant (assumed conservative) forces?[/QUOT

Thank you for responding! :)

yeah... I'm not really good with Calculus...
IF those equation don't work then I think I have to use the following equation.

F = dU/dx
U = ∫F dx

but How do I integrate tho since the function of force is not given?

 

[voko]

How do I integrate tho since the function of force is not given?

It is given, via the diagram.

 

[bestchemist]

It is given, via the diagram.

since the slope from 0 to 0.5 is 4 then the force is F = 4x and the integral of that is 2x² right?
from 0.5 to 1 the force is what? since the slope there is -4, will it be F=-4x?

 

[PhanthomJay]

since the slope from 0 to 0.5 is 4 then the force is F = 4x and the integral of that is 2x² right?

yes, it is actually 2x^2 + k, where k is a constant, and since U =0 when x is 0, then k is 0, so U = 2x^2 between x = 0 and x = 0.5, an upward facing parabola

from 0.5 to 1 the force is what? since the slope there is -4, will it be F=-4x?

Not quite, are you familiar with the equation of a straight line , y = mx + b, where m is the slope of the line and b is the value of y at x = 0 (the y-intercept of the extended line)?

 

[bestchemist]

Not quite, are you familiar with the equation of a straight line , y = mx + b, where m is the slope of the line and b is the value of y at x = 0 (the y-intercept of the extended line)?

Soooo... From 0.5 to 1, F = -4x +4 since the force at 0.5 is 2 so the y intercept is 4!
And then the integral of F will be U=-(2x^2+4x +k) right??
But somehow when I graph this U graph... It doesn't look right. When I plug 0.6 in for x I got 3.12
I have a feeling that its wrong :( can someone please help.

 

[voko]

When you have $$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$ then what is $$ \int_0^x f(x) dx $$?

 

[PhanthomJay]

Soooo... From 0.5 to 1, F = -4x +4 since the force at 0.5 is 2 so the y intercept is 4!

yes

And then the integral of F will be U=-(2x^2+4x +k) right??

you mean U = -2x^2 +4x + k, I think, where k can be found using the knowledge gained in the first part, U = 0.5 when x = 0.5, solve for k.

But somehow when I graph this U graph... It doesn't look right. When I plug 0.6 in for x I got 3.12

Try again, using the corrected equation for U.

Don't forget you then still need to graph the PE from x =1 to x = 1.1.

As a check of your calculus, remember that the area under the force-displacement curve from F=0 to F=x, is the PE at x.

I'm not so good at calculus, either, just the basics. Haven't used it much since college days.

 

[bestchemist]

When you have $$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$ then what is $$ \int_0^x f(x) dx $$?

yes you mean U = -2x^2 +4x + k, I think, where k can be found using the knowledge gained in the first part, U = 0.5 when x = 0.5, solve for k. Try again, using the corrected equation for U.

Don't forget you then still need to graph the PE from x =1 to x = 1.1.

As a check of your calculus, remember that the area under the force-displacement curve from F=0 to F=x, is the PE at x.

I'm not so good at calculus, either, just the basics. Haven't used it much since college days.

Thank you guys,

I think I got it!

but for x=1 to x=1.1
isn't the force is zero so the PE is zero too? the slope is zero so F=0 integral of that will be zero too isn't it?

 

[voko]

but for x=1 to x=1.1
isn't the force is zero so the PE is zero too? the slope is zero so F=0 integral of that will be zero too isn't it?

Zero derivative does not mean that the function is zero. You want your potential energy to be a smooth function, so it should not be zero at x > 1 because it was not zero at x < 1.

 

[bestchemist]

Zero derivative does not mean that the function is zero. You want your potential energy to be a smooth function, so it should not be zero at x > 1 because it was not zero at x < 1.

Sooo
∫F= 0
so U = 0x +k
so U =1?

 

[voko]

Can you answer the question in #8?

 

[bestchemist]

Can you answer the question in #8?

nope :(
I got a(x) and b(x) but I don't know c(x)

 

[voko]

c(x) = 0, as given.

 

[bestchemist]

c(x) = 0, as given.

U = ∫₁^1.1 0
U= 0x + k
isn't it?

 

[voko]

$U = \int_{1}^{1.1} 0 dx$ has almost nothing to do with $U = \int_0^x f(x) dx$ as requested in #8. It cannot be the answer.

 

[bestchemist]

$U = \int_{1}^{1.1} 0 dx$ has almost nothing to do with $U = \int_0^x f(x) dx$ as requested in #8. It cannot be the answer.

I don't know what could it be then
I feel discourage :(
Can you tell me the answer and how you get it step by step, please...

 

[voko]

You need to find this: $$ U(x) = - \int_0^x f(x) dx $$ The complication is that $f(x)$ is not defined as a simple formula:
$$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$

Obviously, when $0 \le x < 0.5$, you can say $U(x) = - \int_0^x a(x) dx$.

But when $x > 0.5$, you cannot say that $U(x) = \int_0^x a(x) dx$, nor can you say that $U(x) = \int_0^x b(x) dx$. However, for any $f(x)$ you can say $\int_0^x f(x) dx = \int_0^{0.5} f(x) dx + \int_{0.5}^x f(x) dx$, so, for $0.5 \le x < 1, \ U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx$.

Now you have to find $U(x)$ for $x \ge 1$.

 

[bestchemist]

You need to find this: $$ U(x) = - \int_0^x f(x) dx $$ The complication is that $f(x)$ is not defined as a simple formula:
$$ f(x) = \begin{cases} a(x), 0 \le x < 0.5 \\ b(x), 0.5 \le x < 1 \\ c(x) \end{cases} $$

Obviously, when $0 \le x < 0.5$, you can say $U(x) = - \int_0^x a(x) dx$.

But when $x > 0.5$, you cannot say that $U(x) = \int_0^x a(x) dx$, nor can you say that $U(x) = \int_0^x b(x) dx$. However, for any $f(x)$ you can say $\int_0^x f(x) dx = \int_0^{0.5} f(x) dx + \int_{0.5}^x f(x) dx$, so, for $0.5 \le x < 1, \ U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx$.

Now you have to find $U(x)$ for $x \ge 1$.

so for x>1
U(x) = -∫₀ ^0.5 ax dx - ∫_0.5 ¹ bx dx - ∫₁^x cx dx

right?

 

[voko]

so for x>1
U(x) = -∫₀ ^0.5 ax dx - ∫_0.5 ¹ bx dx - ∫₁^x cx dx

right?

Right!

 

[bestchemist]

Right!

Thank! Finally! let's me try to graph this thing and see it I get it right!
Thanks again! you're awesome!

 

[voko]

Just for the record, can you show your formulae for the potential energy in all the three intervals?

 

[bestchemist]

Just for the record, can you show your formulae for the potential energy in all the three intervals?

from 0<x<0.5
U = -2x²

from 0.5<x<1
U = -2x^2 +4x + k
k = -1
so U = -2x² +4x - 1

and for x >1

U(x) = -∫₀^0.5 ax dx - ∫_0.5¹ bx dx - ∫₁^x cx dx
U = - 2x<sup>2 - ( -2x2 +4x -1)
U = -4x + 1

Is it right?</sup>

 

[voko]

from 0<x<0.5
U = -2x²

Correct. So $\int_0^x a(x) dx = 2x^2$.

from 0.5<x<1
U = -2x^2 +4x + k
k = -1
so U = -2x² +4x - 1

This is supposed to be $- \int_0^{0.5} a(x) dx - \int_{0.5}^{x} b(x) dx$. From the above, $\int_0^{0.5} a(x) dx = 0.5$. What is $\int_{0.5}^{x} b(x) dx$?

and for x >1

U(x) = -∫₀^0.5 ax dx - ∫_0.5¹ bx dx - ∫₁^x cx dx
U = - 2x^{2 - ( -2x2 +4x -1)
U = -4x + 1}

<sup>You equate U with various different things here, so I am not sure I understand what you are saying here.

If $U = -4x + 1$ is the end result, it is wrong, because when $x > 1$, the force is zero, so the potential energy has to be constant.</sup>

 

[bestchemist]

Correct. So $\int_0^x a(x) dx = 2x^2$.



This is supposed to be $- \int_0^{0.5} a(x) dx - \int_{0.5}^{x} b(x) dx$. From the above, $\int_0^{0.5} a(x) dx = 0.5$. What is $\int_{0.5}^{x} b(x) dx$?



You equate U with various different things here, so I am not sure I understand what you are saying here.

If $U = -4x + 1$ is the end result, it is wrong, because when $x > 1$, the force is zero, so the potential energy has to be constant.

For x >0.5

U = -2x^2 - (-2x^2 +4x-1)
U = -4x +1

for X >1 since it is suppose to be constant

U = -4x +1 -(-4x+1)

I guess on this last one lol...Idk what should it be

 

[voko]

For x >0.5

U = -2x^2 - (-2x^2 +4x-1)
U = -4x +1

Why? I asked a specific question about $\int_{0.5}^{x} b(x) dx$. Answering it would be helpful for you.

 

[bestchemist]

Why? I asked a specific question about $\int_{0.5}^{x} b(x) dx$. Answering it would be helpful for you.

for x >0.5
F= -4x+4
so ∫f dx

U = - 2x^2 +4x +k

∫_0.5¹ -4x+4

isn't it?

 

[voko]

You are getting confused because you use the same letters to denote multiple things. Let $B(x) = \int_{0.5}^{x} b(x) dx$. What is $B(x)$, if $b(x) = -4x + 4$? What is $U(x)$, when $0.5 \le x < 1$?

 

[bestchemist]

You are getting confused because you use the same letters to denote multiple things. Let $B(x) = \int_{0.5}^{x} b(x) dx$. What is $B(x)$, if $b(x) = -4x + 4$? What is $U(x)$, when $0.5 \le x < 1$?

sooo
U = -2x^2 +4x +k ]^x - ( (-2x^2 +4x +k)]^0.5)

right?

 

[voko]

sooo
U = -2x^2 +4x +k ]^x - ( (-2x^2 +4x +k)]^0.5)

right?

Compare this with #19.

 

[bestchemist]

Compare this with #19.

idk now... I'm really confused now :(

 

[HallsofIvy]

For this problem, where the force function is a "broken line", you don't really need "Calculus". The integral is the same as "area under the curve" so, here, all you need is the formula for area of a triangle.

For x between 0 and 0.5, F is given by F= 4x. The "area under the curve" from 0 to x is the area of a right triangle with legs of length "x" and "4x" so area (1/2)(x)(4x)= 2x^2.

Beyond x= 0.5, for x between 0.5 and x= 1, F= 4- 4x. The "area under the curve" from 1/2 to x is the area of a right triangle with legs of length "x- 0.5" and "4- 4x". The "area under the curve" from 1/2 to x is (1/2)(x- 0.5)(4- 4x)= (x- 1/2)(2- 2x)= -2x^2+ 3x- 1. The "area under the curve" from 0 to x, for x> 1/2, is the area from 0 to 1/2 which is 1/2, plus the area of the second triangle.

 

[bestchemist]

For this problem, where the force function is a "broken line", you don't really need "Calculus". The integral is the same as "area under the curve" so, here, all you need is the formula for area of a triangle.

For x between 0 and 0.5, F is given by F= 4x. The "area under the curve" from 0 to x is the area of a right triangle with legs of length "x" and "4x" so area (1/2)(x)(4x)= 2x^2.

Beyond x= 0.5, for x between 0.5 and x= 1, F= 4- 4x. The "area under the curve" from 1/2 to x is the area of a right triangle with legs of length "x- 0.5" and "4- 4x". The "area under the curve" from 1/2 to x is (1/2)(x- 0.5)(4- 4x)= (x- 1/2)(2- 2x)= -2x^2+ 3x- 1. The "area under the curve" from 0 to x, for x> 1/2, is the area from 0 to 1/2 which is 1/2, plus the area of the second triangle.

so from x = 0 to 0.5 I'll use 2x^2 to graph
anf for x = 0.5 to 1 I'll have to use -3x +1? since 2x^2 - (-2x^2 +3x -1) = -3x+1

 

[voko]

idk now... I'm really confused now :(

In #19: $U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx , \ 0.5 \le x < 1$.

In #30, you found what $\int_{0.5}^x b(x) dx$ is. You still need to compute $\int_0^{0.5} a(x) dx$ (which is the area of a triangle, as HallsofIvy remarked), and you need to mind the signs when plug all this into the formula for $U(x)$.

 

[bestchemist]

In #19: $U(x) = - \int_0^{0.5} a(x) dx - \int_{0.5}^x b(x) dx , \ 0.5 \le x < 1$.

In #30, you found what $\int_{0.5}^x b(x) dx$ is. You still need to compute $\int_0^{0.5} a(x) dx$ (which is the area of a triangle, as HallsofIvy remarked), and you need to mind the signs when plug all this into the formula for $U(x)$.

okay so..
from taking the integral of a and b I got
2x^2 -2x^2+4x+k +1/2-2-k

then U = 4x+5/2

I think I did it wrong again...:(

 

[voko]

okay so..
from taking the integral of a and b I got
2x^2 -2x^2+4x+k +1/2-2-k

then U = 4x+5/2

I think I did it wrong again...:(

You computed indefinite integrals correctly. But the formula needs definite integrals, and it is important to use correct limits, which you mostly ignore, except in #30, where you did use them - correctly.

And you need to mind the signs. Potential energy is defined with a minus sign, which, unfortunately for you, makes things more confusing than they already are. But you are on the right track, so don't give up just yet.

 

[bestchemist]

You computed indefinite integrals correctly. But the formula needs definite integrals, and it is important to use correct limits, which you mostly ignore, except in #30, where you did use them - correctly.

And you need to mind the signs. Potential energy is defined with a minus sign, which, unfortunately for you, makes things more confusing than they already are. But you are on the right track, so don't give up just yet.

so...

-2x^2 - ((-2x^2 +4x+k)]^x - (-2x^2 +4x-k)}^0.5)

does this look right??

 

[voko]

so...

-2x^2 - ((-2x^2 +4x+k)]^x - (-2x^2 +4x-k)}^0.5)

does this look right??

Almost. The first term should have been $-2x^2 |_{0}^{0.5}$ - see the difference?

 

[bestchemist]

Almost. The first term should have been $-2x^2 |_{0}^{0.5}$ - see the difference?

ohhh... yep I see it now... I didn't look at the limit like you said...
does the first term is -1/2 then since -2x^2 ]^0.5 = -1/2

how about from x -1 to 1 then... how will the function become constant since there are so many variable here

 

[voko]

ohhh... yep I see it now... I didn't look at the limit like you said...
does the first term is -1/2 then since -2x^2 ]^0.5 = -1/2

Correct. So what is the complete formula for $0.5 \le x < 1$?

how about from x -1 to 1 then... how will the function become constant since there are so many variable here

You mean "x > 1"?

You got the general formula in #20. Use it, paying attention to the limits and signs.

 

[bestchemist]

Correct. So what is the complete formula for $0.5 \le x < 1$?



You mean "x > 1"?

You got the general formula in #20. Use it, paying attention to the limits and signs.

okay... so If I did it right

U = 2x^2 -4x-2

and for x >1
I did the calculation and I'm so sure about it lol

U = -1

right?

 

[voko]

okay... so If I did it right

U = 2x^2 -4x-2

Not quite. The "-2" in the end is wrong. I think you got lost in the signs, check them.

An easy way to check whether you formula is correct: the potential energy is smooth, so the value at 0.5 must be the same calculated from either x < 0.5 or x > 0.5. Approaching from x < 0.5, the value is $-2x^2 = -0.5$; approaching it from x > 0.5, your formula gives $2x^2 - 4x - 2 = -3.5$, so it must be wrong.

and for x >1
I did the calculation and I'm so sure about it lol

U = -1

right?

Yes!

Note that this is the (negative) area of the entire force triangle, just like it should be.

 

[bestchemist]

Not quite. The "-2" in the end is wrong. I think you got lost in the signs, check them.

An easy way to check whether you formula is correct: the potential energy is smooth, so the value at 0.5 must be the same calculated from either x < 0.5 or x > 0.5. Approaching from x < 0.5, the value is $-2x^2 = -0.5$; approaching it from x > 0.5, your formula gives $2x^2 - 4x - 2 = -3.5$, so it must be wrong.



Yes!

Note that this is the (negative) area of the entire force triangle, just like it should be.

okie, so
U = -2x^2 -4x +2
right?
If x = 0.5, then U = -2(0.5)^2 -4(0.5)+2
U=-0.5

 

[voko]

okie, so
U = -2x^2 -4x +2
right?

Sorry, no. The formula is $- \int_0^{0.5} 4x dx - \int_{0.5}^x (4 - 4x) dx$, so this is $- \text{some number} + 2x^2 - 4x + \text{some other number}$. Note that it is $2x^2$, not $-2x^2$.

 

[bestchemist]

Sorry, no. The formula is $- \int_0^{0.5} 4x dx - \int_{0.5}^x (4 - 4x) dx$, so this is $- \text{some number} + 2x^2 - 4x + \text{some other number}$. Note that it is $2x^2$, not $-2x^2$.

I think I got it... lol

U = 2x^2 -6x +2

x = 0.5

U = 2(0.5)^2 -6(0.5)+2
U =-0.5

Right?

 

[voko]

Per #45, there must be -4x, not +6x.

 

[bestchemist]

Per #45, there must be -4x, not +6x.

I think I got it for real this time... lol sooo much confident lol

U = 2x^2 -4x +1

Right?

 

[voko]

Right!

 

[bestchemist]

Right!

yayyyyyyyyyyyy...
After a few days on this one problem... Finally got it lol
Thank you so much!