cde42003
- 22
- 0
Can anyone help me with theses problems?
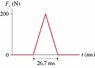
1. A 500 g cart is released from rest 1.0 m from the bottom of a frictionless, 30 ramp. The cart rolls down the ramp and bounces off a rubber block at the bottom. The figure shows the force during the collision.
After the cart bounces, how far does it roll back up the ramp?
On this one I know I need to solve for the velocities before and after the collision and then use this value to get the distance, but I am not sure as to how I need to do this. I don't really know how to get the acceleration.
2. In a military test, a 575 kg unmanned spy plane is traveling north at an altitude of 2700 m and a speed of 450 m/s. It is intercepted by a 1280 kg rocket traveling east at 725 m/s.
If the rocket and the spy plane become enmeshed in a tangled mess, how far from the point of impact do they hit the ground?
This problem really has me puzzled. I tried to use the m1v1 + m2v2= m(1+2)v equation and solve for the magnitude of the velocity but am not sure where to go from there. Let me know where I went wrong. Thanks
1. A 500 g cart is released from rest 1.0 m from the bottom of a frictionless, 30 ramp. The cart rolls down the ramp and bounces off a rubber block at the bottom. The figure shows the force during the collision.
After the cart bounces, how far does it roll back up the ramp?
On this one I know I need to solve for the velocities before and after the collision and then use this value to get the distance, but I am not sure as to how I need to do this. I don't really know how to get the acceleration.
2. In a military test, a 575 kg unmanned spy plane is traveling north at an altitude of 2700 m and a speed of 450 m/s. It is intercepted by a 1280 kg rocket traveling east at 725 m/s.
If the rocket and the spy plane become enmeshed in a tangled mess, how far from the point of impact do they hit the ground?
This problem really has me puzzled. I tried to use the m1v1 + m2v2= m(1+2)v equation and solve for the magnitude of the velocity but am not sure where to go from there. Let me know where I went wrong. Thanks