MatPhy
- 4
- 0
Hello everybody!
I know how to solve Laplace equation on a square or a rectangle.
Is there any easy way to find an analytical solution of Laplace equation on a trapezoid (see picture).
Thank you.
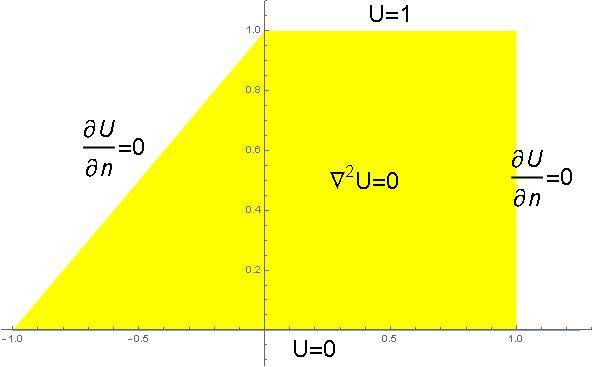
I know how to solve Laplace equation on a square or a rectangle.
Is there any easy way to find an analytical solution of Laplace equation on a trapezoid (see picture).
Thank you.