How to Solve Two Masses Connected by a Spring in Ground Frame of Reference?

[NTesla]

Homework Statement

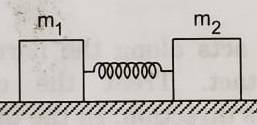
Two blocks of masses m1 and m2 are connected by a spring of spring constant k. The block of mass m1 is pulled by a constant force F1 and the other block is pulled by a constant force F2 in the direction opposite to that of F1. Find the maximum elongation that the spring will suffer.

Relevant Equations

Newton's laws of motion

I have solved this question in Center of mass frame of reference, by using energy conservation. However, I'm not able to write any equation when I'm trying to solve it in Ground frame of reference. Can somebody please let me know how to begin in Ground FoR.

 

[anuttarasammyak]

After reaching the maximum elongation x, m_1 and m_2 moves with same acceleration of
$\frac{F_1-F_2}{m_1+m_2}$. By the two forces with force from spring T which is kx you can write down equation of motion and get x.

 

[NTesla]

After reaching the maximum elongation x, m_1 and m_2 moves with same acceleration of
$\frac{F_1-F_2}{m_1+m_2}$. By the two forces with force from spring T which is kx you can write down equation of motion and get x.

$\frac{F_1-F_2}{m_1+m_2}$ is the acceleration of the center of mass of the system; not that of individual masses. The center of mass will move with this acceleration when viewed from Ground frame. However, individual masses will be in simple harmonic motion. The acceleration of individual masses will be different from that of CoM.

 

[anuttarasammyak]

I thought once extended to the maximum the spring becomes as the rod so the two body are regarded as one body.
F_1-T=m_1 a_1
T-F_2=m_2 a_2
and at last
a_1=a_2=\frac{F_1-F_2}{m_1+m_2}

I am interested to know your result of oscillation.

EDIT : Thanks to advice of harupsex I understand I was wrong getting to know $T=k(x_1-x_2-l)$.
Rewriting the equation of motion as
m_1 \ddot{x_1}=k(x_2-x_1-l_0)+F_1
m_2 \ddot{x_2}=-k(x_2-x_1-l_0)+F_2
where $x_1<x_2$, $l_0$ is natural length of spring and positive direction of $F_1,F_2$ is same as it of x. By adding these equations side by side
\ddot{x_G}=\frac{F_1+F_2}{m_1+m_2}
where
x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}
is coordinate of CoM.

Rewriting the equations as
\ddot{x_1}=k/m_1\ (x_2-x_1-l_0)+F_1/m_1
\ddot{x_2}=-k/m_2\ (x_2-x_1-l_0)+F_2/m_2
Deleting side by side
\ddot{(x_2-x_1)}=-k(1/m_1+1/m_2)(x_2-x_1-l_0)+F_2/m_2-F_1/m_1
\ddot{(x_2-x_1-l)}=-k(1/m_1+1/m_2)(x_2-x_1-l)=-\omega^2 (x_2-x_1-l)
where
l-l_0=\frac{F_2/m_2-F_1/m_1}{\omega^2}
\omega^2=k(1/m_1+1/m_2)
With initial conditions
x_1(t=0),x_2(0),\dot{x_1}(0),\dot{x_2}(0)
given we get amplitude of the harmonic oscillation A. Then the maximum elongation would be
A+|l-l_0|=A+|\frac{F_2/m_2-F_1/m_1}{\omega^2}|
As an example for
x_2(0)-x_1(0)=l_0,\dot{x_1}(0)=0,\dot{x_2}(0)=0
$A=|l-l_0|$ so the maximum elongation is $2|l-l_0|$.

 

[haruspex]

After reaching the maximum elongation x, m_1 and m_2 moves with same acceleration of
$\frac{F_1-F_2}{m_1+m_2}$.

No, at maximum elongation the two masses will have the same velocity but will be accelerating towards each other.

 

[haruspex]

I'm not able to write any equation when I'm trying to solve it in Ground frame of reference. Can somebody please let me know how to begin in Ground FoR.

I'm having to guess at exactly what you did, so if what I write makes no sense please post your working.
You can still write the energy equation, but you get extra unknowns: the velocity of the mass centre and two displacements instead of one. So you need more equations. Introducing time as yet another unknown allows you to write equations for the mass centre's velocity and displacement. That appears to leave you one equation short, but it turns out that you can find the spring extension.

 

[NTesla]

I've tried to attempt this question from Ground frame of reference, but not able to move towards solution. Here's my attempt:

 

[haruspex]

I've tried to attempt this question from Ground frame of reference, but not able to move towards solution. Here's my attempt:
View attachment 272705

Since you solved it using energy in the CoM frame, I thought you were looking to solve it in the ground frame without handling the forces on the blocks separately.
I had as positions the displacements to left and right of the two blocks, but your r variables should work as well.
I wrote an energy equation, thereby bringing in the common velocity of the blocks, a momentum equation relating that to the elapsed time, and an equation relating the time and the external forces to the displacement of the mass centre. That was enough to get me an answer.

 

[NTesla]

When I solved this question using the CoM FoR, the maximum extension of the spring came to be = $\frac{2}{k}(\frac{F_1m_2+F_2m_1}{m_1+m_2})$

Is this what you've also got as maximum extension of the spring ?

Since there is a net force in the horizontal direction, therefore momentum conservation cannot be used.
Please guide me as to how the 3 equation that you've written could be approached.

 

[haruspex]

Since there is a net force in the horizontal direction, therefore momentum conservation cannot be used.

I introduced time as a variable. That allows you to write the change in momentum.

 

[Delta2]

Is it totally wrong to try to solve for $x_1(t),x_2(t)$ by applying Newton's 2nd for each body? It seems we get a coupled system of ODEs, i suppose there isn't a closed form for $x_1(t),x_2(t)$??

Or can we assume the solution ansatz $x_i(t)=A_i\sin(\omega t+\phi_i)$ and proceed to determine $A_i,\phi_i$?

 

[haruspex]

Is it totally wrong to try to solve for $x_1(t),x_2(t)$ by applying Newton's 2nd for each body? It seems we get a coupled system of ODEs, i suppose there isn't a closed form for $x_1(t),x_2(t)$??

Or can we assume the solution ansatz $x_i(t)=A_i\sin(\omega t+\phi_i)$ and proceed to determine $A_i,\phi_i$?

That'll work, of course, but as I read post #1, @NTesla is looking for how to use the simpler holistic approach, using energy etc., but in the ground frame.

 

[NTesla]

Since you solved it using energy in the CoM frame, I thought you were looking to solve it in the ground frame without handling the forces on the blocks separately.
I had as positions the displacements to left and right of the two blocks, but your r variables should work as well.
I wrote an energy equation, thereby bringing in the common velocity of the blocks, a momentum equation relating that to the elapsed time, and an equation relating the time and the external forces to the displacement of the mass centre. That was enough to get me an answer.

Could you please tell that which event have you taken as the beginning of time, when writing the momentum equation..?

 

[haruspex]

Could you please tell that which event have you taken as the beginning of time, when writing the momentum equation..?

To solve the question at all, I think you have to assume the blocks start at rest with the spring at its relaxed length.

 

[NTesla]

I'm rethinking about the problem. Suppose that the Force F1 and F2 are applied to the massess m1 and m2 by holding the force applying agents with hand, so that the spring only stretches to its max limit, and then doesn't contract. Then the masses will not be in SHM. Then we can just equate work done by the forces to the potential energy in the spring.
But if the Forces are applied on m1 and m2 suddenly, then the masses will definitely will be in SHM. This will make the situation complex.
Am I right in supposing like so..?

 

[haruspex]

I'm rethinking about the problem. Suppose that the Force F1 and F2 are applied to the massess m1 and m2 by holding the force applying agents with hand, so that the spring only stretches to its max limit, and then doesn't contract. Then the masses will not be in SHM. Then we can just equate work done by the forces to the potential energy in the spring.
But if the Forces are applied on m1 and m2 suddenly, then the masses will definitely will be in SHM. This will make the situation complex.
Am I right in supposing like so..?

I think you are supposed to assume as I wrote in post #15. Consequently, the masses will overshoot the equilibrium position.
If you use the approach I outlined in post #8, you can solve it without invoking SHM.

 

[NTesla]

I've written an impulse momentum equation:
$$(F_{2}-F_{1})\Delta t=(m_1+m_2)v_{com}=m_1v_1+m_2v_2$$
$\Delta t$ = time difference starting from unstretched position to position of maximum stretch of spring.
I am assuming that maximum stretch will happen when $v_1$ = $v_2$ = $v_{com}$ = $\frac{m_1v_1+m_2v_2}{m_1+m_2}$
Next I've written an energy equation:
$$\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+\frac{1}{2}k(x_1+x_2)^2=(F_2-F_1)\frac{(F_2-F_1)}{m_1+m_2}\Delta t$$

Please let me know, if I've written the correct equations.

 

[anuttarasammyak]

Hi. momentum equation is
(F_1+F_2)t=m_1 \dot{x_1}(t)+m_2 \dot{x_2}(t) - m_1 \dot{x_1}(0)-m_2 \dot{x_2}(0)
same as yours, where I take positive directions of both $F_1$ and $F_2$ are same as that of x for simplicity. From this equation gives velocity of the CoM.
(\frac{\dot{m_1 x_1 +m_2 x_2}}{m_1+m_2})=\frac{F_1+F_2}{m_1+m_2}t+(\frac{m_1 \dot{x_1}(0) +m_2 \dot{x_2}(0)}{m_1+m_2})Energy equation is
F_1(x_1(t)-x_1(0))+F_2(x_2(t)-x_2(0))=\frac{1}{2}m_1(\dot{x_1}(t)^2-\dot{x_1}(0)^2) + \frac{1}{2}m_2(\dot{x_2}(t)^2-\dot{x_2}(0)^2)+\frac{1}{2}k[( x_2(t)-x_1(t)-l_0)^2-( x_2(0)-x_1(0)-l_0)^2]
where $l_0$ is natural length of the spring, $x_1<x_2$.

 

[haruspex]

I've written an impulse momentum equation:
$$(F_{2}-F_{1})\Delta t=(m_1+m_2)v_{com}=m_1v_1+m_2v_2$$
$\Delta t$ = time difference starting from unstretched position to position of maximum stretch of spring.
I am assuming that maximum stretch will happen when $v_1$ = $v_2$ = $v_{com}$ = $\frac{m_1v_1+m_2v_2}{m_1+m_2}$
Next I've written an energy equation:
$$\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+\frac{1}{2}k(x_1+x_2)^2=(F_2-F_1)\frac{(F_2-F_1)}{m_1+m_2}\Delta t$$

Please let me know, if I've written the correct equations.

I don't understand the RHS of your energy equation. Its dimension seems to be power, not energy.
As @anuttarasammyak posts, you need to involve the work done by the forces in going through their displacements.

And as I wrote, you need another equation relating the acceleration of the mass centre to its displacement and the elapsed time.

 

[NTesla]

Hi. momentum equation is
(F_1+F_2)t=m_1 \dot{x_1}(t)+m_2 \dot{x_2}(t) - m_1 \dot{x_1}(0)-m_2 \dot{x_2}(0)
same as yours, where I take positive directions of both $F_1$ and $F_2$ are same as that of x for simplicity. From this equation gives velocity of the CoM.
(\frac{\dot{m_1 x_1 +m_2 x_2}}{m_1+m_2})=\frac{F_1+F_2}{m_1+m_2}t+(\frac{m_1 \dot{x_1}(0) +m_2 \dot{x_2}(0)}{m_1+m_2})Energy equation is
F_1(x_1(t)-x_1(0))+F_2(x_2(t)-x_2(0))=\frac{1}{2}m_1(\dot{x_1}(t)^2-\dot{x_1}(0)^2) + \frac{1}{2}m_2(\dot{x_2}(t)^2-\dot{x_2}(0)^2)+\frac{1}{2}k[( x_2(t)-x_1(t)-l_0)^2-( x_2(0)-x_1(0)-l_0)^2]
where $l_0$ is natural length of the spring, $x_1<x_2$.

In your energy equation, I have some difficulty: Change in kinetic energy of a system of particles is equal to work done by ALL the external force on the system. Here, the spring is getting extended by $x_1+x_2$, supposing that the mass $m_1$ moves by $x_1$ and mass $m_2$ moves by $x_2$. But how much the mass $m_1$ has moved solely due to $F_1$ or how much the mass $m_2$ moved solely due to $F_2$ is not available. Moreover, when viewed from Ground Frame of reference, the mass $m_1$ has moved NOT just by $x_1$, but by $(x_1+ the~distance~moved~by~CoM).$ Likewise for $m_2$.

@haruspex , In my energy equation, in post # 17, in RHS, I've written work done = Force*displacement. $F_2-F_1$ is the net external force on the system, and displacement of the system's com is 0.5*acceleration*$time^2$. Acceleration is $\frac{F_2-F_1}{m_1+m_2}$, time is $\Delta t$. Time should have been squared in post #17 and RHS should have been multiplied by 0.5 .

 

[haruspex]

@haruspex , In my energy equation, in post # 17, in RHS, I've written work done = Force*displacement. $F_2-F_1$ is the net external force on the system, and displacement of the system's com is 0.5*acceleration*$time^2$. Acceleration is $\frac{F_2-F_1}{m_1+m_2}$, time is $\Delta t$. Time should have been squared in post #17 and RHS should have been multiplied by 0.5 .

Ok, that explains the dimensionality error, but it is still wrong.

The LHS is the total work done on the system, whereas the RHS is only the work done in accelerating the common mass centre.
To see this, consider the case where the masses are equal and so are the forces. Your RHS becomes zero, but work has been done both in stretching the spring and giving KE to the individual masses.

Instead, consider the displacement each force goes through.

 

[anuttarasammyak]

Hi.

Change in kinetic energy of a system of particles is equal to work done by ALL the external force on the system.

You should not forget potential energy of spring. Change in the sum of kinetic energy of a system of particles and potential energy of spring is equal to work done by ALL the external force on the system.

Here, the spring is getting extended by x1+x2, supposing that the mass m1 moves by x1 and mass m2 moves by x2

The spring gets extented by $x_2(t)-x_1(t)-l_0$ from its natural length.

But how much the mass m1 has moved solely due to F1 or how much the mass m2 moved solely due to F2 is not given.

Sum of external force and spring force keep applying on the blocks. There happens no such a thing as "move solely due to one force".

Moreover, when viewed from Ground Frame of reference, the mass m1 has moved NOT just by x1, but by (x1+the distance moved by CoM). Likewise for m2.

All the above $x_1$ and $x_2$ are coordinates mentioning the position of the particle like blocks in ground frame of reference. We do not have to care about "CoM distance moved" for our problem.

 

[NTesla]

@anuttarasammyak
In post#4:
$l$ being the length of the string at any point of time, I couldn't understand how you substituted the variable $l$ in this equation from the previous equation: \ddot{(x_2-x_1-l)}=-k(1/m_1+1/m_2)(x_2-x_1-l)=-\omega^2 (x_2-x_1-l)

Also, for what reasons have you written that the maximum elongation would be
A+|l-l_0|

 

[anuttarasammyak]

Hi. Please try to guess if it seems right to you.

Hint: oscillation of spring upside fixed on ceiling downside put weight in gravitation field.

 

[NTesla]

@anuttarasammyak: In the following equtions that you've written in post#4, please explain what have you considered $x_1$ and $x_2$ to be. My understanding is that $x_1$ and $x_2$ is the displacement of mass $m_1$ and $m_2$. If it is so, then stretch of string at any point of time will be $x_1+x_2$. Then, why have you written the following equations in post#4, considering $x_2-x_1-l_0$ as the stretch of the string:
m_1 \ddot{x_1}=k(x_2-x_1-l_0)+F_1
m_2 \ddot{x_2}=-k(x_2-x_1-l_0)+F_2

 

[NTesla]

@haruspex,
I've written the momentum equation:
$$\left ( F_2-F_1 \right)\Delta t=\left ( m_1+m_2 \right )v_{com}=m_1v_1+m_2v_2$$
and Energy equation :
$$F_1x_1+F_2x_2=\frac{1}{2}m_1v_1^{2}+\frac{1}{2}m_2v_2^{2}+\frac{1}{2}k\left ( x_1+x_2 \right )^{2}$$

But if I write another equation involving displacement and time, like following:
$$\Delta s=\frac{1}{2}\left ( \frac{F_2-F_1}{m_1+m_2} \right )\Delta t^2$$
then I'm including one more variable $\Delta s$.
I am not able to write an equation involving displacement and time which doesn't involve a new variable. Where am I going wrong. Please help.

 

[anuttarasammyak]

Hi.

m_1 \ddot{x_1}=k(x_2-x_1-l_0)+F_1
m_2 \ddot{x_2}=-k(x_2-x_1-l_0)+F_2

Please find attached my configuration. I hope it will help you.

 

[NTesla]

@anuttarasammyak, Ok, now I understand those 2 equations. Thank you.
But, I still have one question: In the following equation that you've written in post#4:
\ddot{(x_2-x_1-l)}=-k(1/m_1+1/m_2)(x_2-x_1-l)=-\omega^2 (x_2-x_1-l)
$l$= total length of the string at any instant t=$x_2-x_1-l_0$
Therefore, $(\ddot{x_2-x_1-l})$=$(\ddot{x_2-x_1-(x_2-x_1-l_0)})$=$(\ddot{-2x_1+l_0})$. This doesn't make sense to me. Please explain this particular equation that you've written.

 

[haruspex]

then I'm including one more variable Δs.

That's the displacement of the mass centre. How does that relate to m₁, m₂, x₁ and x₂?

 

[anuttarasammyak]

@anuttarasammyak,
(x2−x1−l)¨=−k(1/m1+1/m2)(x2−x1−l)=−ω2(x2−x1−l)
l= total length of the string at any instant t=x2−x1−l0
Therefore, (x2−x1−l¨)=(x2−x1−(x2−x1−l0)¨)=(−2x1+l0¨). This doesn't make sense to me. Please explain this particular equation that you've written.

\ddot{(x_2-x_1)}=-k(1/m_1+1/m_2)(x_2-x_1-l_0)+F_2/m_2-F_1/m_1

You see RHS second term $F_2/m_2-F_1/m_1$ is constant.

You see RHS first term is written as
-k(1/m_1+1/m_2)(x_2-x_1-l_0)=-k(1/m_1+1/m_2)(x_2-x_1) - k(1/m_1+1/m_2)(-l_0)
the second term is constant.
Add these two constants and express it as
k(1/m_1+1/m_2)l
introducing new constant $l$. Show me expression of $l$ by F,m,k and l_0.

 

[NTesla]

@haruspex ,
I've tried to find a relation between CoM's displacement and $x_1$ and $x_2$, but it appears more difficult than I assumed it to be. Here's my work:

I am not able to figure out the relation. let me know how to proceed.

 

[NTesla]

\ddot{(x_2-x_1)}=-k(1/m_1+1/m_2)(x_2-x_1-l_0)+F_2/m_2-F_1/m_1

You see RHS second term $F_2/m_2-F_1/m_1$ is constant.

You see RHS first term is written as
-k(1/m_1+1/m_2)(x_2-x_1-l_0)=-k(1/m_1+1/m_2)(x_2-x_1) - k(1/m_1+1/m_2)(-l_0)
the second term is constant.
Add these two constants and express it as
k(1/m_1+1/m_2)l
introducing new constant $l$. Show me expression of $l$ by F,m,k and l_0.

@anuttarasammyak, Perhaps I hadn't made the question clear in my earlier post. I do understand the calculation part of it. What I couldn't understand is that what is the physical significance of the variable which you have double differentiated in the equation:

 

[anuttarasammyak]

What I couldn't understand is that what is the physical significance of the variable which you have double differentiated in the equation:

You observe that this is equation of harmonic oscillation : displacement $x_2-x_1-l$, angular frequency $\omega$.

l is new "natural length" of spring with $F_1$ and $F_2$ applied. $x_2-x_1-l$ is extension of spring from renewed balance point. See also HINT in my previous post.

 

[NTesla]

You observe that this is equation of harmonic oscillation : displacement $x_2-x_1-l$, angular frequency $\omega$.

l is new "natural length" of spring with $F_1$ and $F_2$ applied. $x_2-x_1-l$ is extension of spring from renewed balance point. See also HINT in my previous post.

@anuttarasammyak,
Since $x_1, x_2$ are coordinates of masses at any instant.
$l$=$x_2-x_1$. Therefore, $x_2-x_1-l$ = $x_2-x_1-x_2+x_1$ = $0$ always. So there is no reason why this should be differentiated wrt time.

 

[anuttarasammyak]

Since $x_1, x_2$ are coordinates of masses at any instant.
$l$=$x_2-x_1$. Therefore, $x_2-x_1-l$ = $x_2-x_1-x_2+x_1$ = $0$ always. So there is no reason why this should be differentiated wrt time.

You have done the calculation so know that $l$ is constant. So your $l$=$x_2-x_1$ means spring between block 1 and block 2 does not change its length like a rod, though the equation is that of harmonic oscillation. Do I catch you right ?

 

[NTesla]

You have done the calculation so know that $l$ is constant. So your $l$=$x_2-x_1$ means spring between block 1 and block 2 does not change its length like a rod, though the equation is that of harmonic oscillation. Do I catch you right ?

I'm trying to understand your calculation in post #4. You have taken $x_1,x_2$ as coordinates.
$l$ is the length of string at any instant of time. It is not a constant. $l$ changes wrt time.
$l$=$x_2-x_1$, considering that $x_1, x_2$ are coordinates of the masses $m_1$ and $m_2$.
But, the value of $x_2-x_1-l=0$ always.

 

[anuttarasammyak]

Hi. My l is

l-l_0=\frac{F_2/m_2-F_1/m_1}{\omega^2}

Your l is

It is not a constant. $l$ changes wrt time.
$l$=$x_2-x_1$, considering that $x_1, x_2$ are coordinates of the masses $m_1$ and $m_2$.
But, the value of $x_2-x_1-l=0$ always.

So the equation is written as
\ddot{(l_{yours}-l_{mine})}+\omega^2(l_{yours}-l_{mine})=0
where
\omega^2=k(1/m_1+1/m_2)
l_{mine}=l_0+\frac{F_2/m_2-F_1/m_1}{\omega^2}, constant, and
l_{yours}=x_2-x_1=l_{yours}(t) function of time.

$l_{yours}-l_{mine}$ is elongation of spring not from its natural length $l_0$ but from $l_{mine}$ which is interpreted as altered natural length under external constant forces.

 

[haruspex]

@haruspex ,
I've tried to find a relation between CoM's displacement and $x_1$ and $x_2$, but it appears more difficult than I assumed it to be. Here's my work: View attachment 273350

I am not able to figure out the relation. let me know how to proceed.

If m₁ moves x₁ to the left and m₂ moves x₂ to the right then that shifts the "mass moment" m₂ x₂ - m₁ x₁ to the right, so (m₁+m₂)Δs = m₂ x₂ - m₁ x₁, where Δs is positive to the right.

 

[NTesla]

@haruspex, Thank you so much. That was very helpful.

Just one question: If we do not resort to center of mass FoR, and work solely in Ground FoR, then how can we explain that the maximum elongation will happen when both the masses have same velocity as that of velocity of com ?

 

[haruspex]

@haruspex, Thank you so much. That was very helpful.

Just one question: If we do not resort to center of mass FoR, and work solely in Ground FoR, then how can we explain that the maximum elongation will happen when both the masses have same velocity as that of velocity of com ?

Not sure if that's what you meant. There's no problem explaining that; do you mean, how do we use it?
Isn't it the same as saying the two masses have the same velocity?

 

[NTesla]

@haruspex,
When working in CoM FoR, both the masses will seem to be moving in opposite direction and maximum extension in spring will happen when velocity of both the masses is equal to zero at the same instant.

However, when working in Ground FoR, the bodies might seem to be moving in same direction, but maximum extension of spring will happen when both the masses have same speed in same direction. Will it be right to say so.? If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

 

[anuttarasammyak]

Hi.

If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

At extreme points
\dot{l_{yours}}=0
It means
\dot{x_1}=\dot{x_2}
When it is maximum extension
\ddot{l_{yours}}=-\omega^2(l_{yours}-l_{mine})&lt; 0
For minimum shrink
\ddot{l_{yours}}=-\omega^2(l_{yours}-l_{mine})&gt; 0

 

[haruspex]

@haruspex,
When working in CoM FoR, both the masses will seem to be moving in opposite direction and maximum extension in spring will happen when velocity of both the masses is equal to zero at the same instant.

However, when working in Ground FoR, the bodies might seem to be moving in same direction, but maximum extension of spring will happen when both the masses have same speed in same direction. Will it be right to say so.? If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

If the two masses have different velocities in the ground frame then they are either getting closer or further apart. If closer, they must have been further apart earlier; if further apart, they will be at max separation later. So when at max, the relative velocity must be zero.

 

[NTesla]

@anuttarasammyak and @haruspex : Thank you so much. Your contribution was very helpful and is very much appreciated.