- #1
Edward Solomo
- 72
- 1
Suppose I wanted to cut an epicycloid with K cusps (cusps = petals if you think of them as flowers).
http://mathworld.wolfram.com/Epicycloid.html
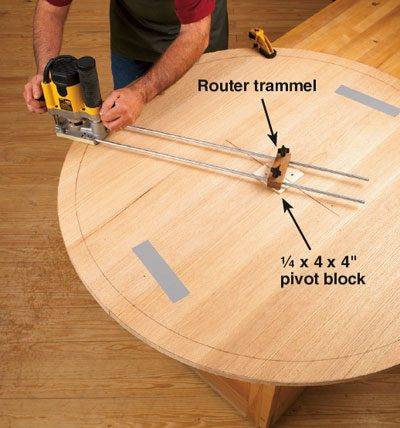
Well, to start simple, suppose we only wanted to cut a circular piece of wood. I would make a trammel with a pin extending through my trammel and the piece of wood I'm cutting. On the opposite end of my trammel, I would place my router at a fix distance from the pin, and then I would either rotate the trammel OR rotate the piece of wood I'm cutting
If we want to cut an ellipse, we modify the trammel in the style of the "Trammel of Archimedes"--------------------------------
Now suppose we want to cut an epicycloid?
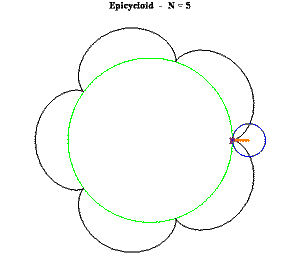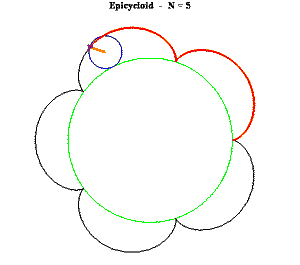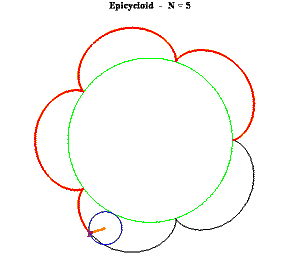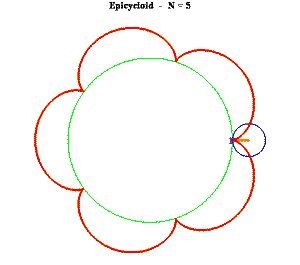
The first idea that comes to mind is to build a small circular trammel and pin it to the endpoint of the primary trammel.
Yet, there is no way to guarantee that both trammels will rotate at their respective rates with such a simple device.
For instance, suppose we want to cut 8 cusps about a circle of radius R. The primary trammel would measure in (9/8)R in length.
Then we attach a second trammel of radius (1/8)R to the endpoint of the primary trammel. Each revolution of the secondary trammel will oscillate between (8/8)R and (10/8R) from the origin of the primary trammel.
However, simply rotating the secondary trammel will not rotate the primary trammel.
In this scenario, the secondary trammel must spin 8 times faster than the primary trammel (which will mathematically generate NINE, not EIGHT, revolutions towards a FIXED point in space).
DELETED the ideas to accomplish this since they were terrible.
-------------------------------------------Any ideas?
http://mathworld.wolfram.com/Epicycloid.html
Well, to start simple, suppose we only wanted to cut a circular piece of wood. I would make a trammel with a pin extending through my trammel and the piece of wood I'm cutting. On the opposite end of my trammel, I would place my router at a fix distance from the pin, and then I would either rotate the trammel OR rotate the piece of wood I'm cutting
If we want to cut an ellipse, we modify the trammel in the style of the "Trammel of Archimedes"--------------------------------
Now suppose we want to cut an epicycloid?
The first idea that comes to mind is to build a small circular trammel and pin it to the endpoint of the primary trammel.
Yet, there is no way to guarantee that both trammels will rotate at their respective rates with such a simple device.
For instance, suppose we want to cut 8 cusps about a circle of radius R. The primary trammel would measure in (9/8)R in length.
Then we attach a second trammel of radius (1/8)R to the endpoint of the primary trammel. Each revolution of the secondary trammel will oscillate between (8/8)R and (10/8R) from the origin of the primary trammel.
However, simply rotating the secondary trammel will not rotate the primary trammel.
In this scenario, the secondary trammel must spin 8 times faster than the primary trammel (which will mathematically generate NINE, not EIGHT, revolutions towards a FIXED point in space).
DELETED the ideas to accomplish this since they were terrible.
-------------------------------------------Any ideas?
Last edited by a moderator: