- #1
Sam Donovan
- 12
- 0
Member advised to do some research before posting
Specifically:
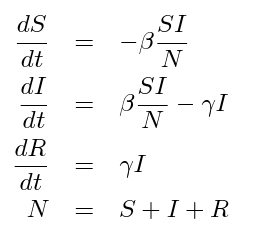
Thank you! Do you think there any sites or wiki articles with the math proof for these equations?fresh_42 said:
Differential equations are used in SIR (Susceptible, Infected, Recovered) models to describe the rate of change of each population group over time. These equations take into account factors like infection rate, recovery rate, and population size to predict how a disease will spread.
The SIR model equation is a set of three differential equations that represent the change in the number of individuals in each population group (susceptible, infected, and recovered) over time. The equation is dS/dt = -βSI, dI/dt = βSI - γI, and dR/dt = γI, where S is the number of susceptible individuals, I is the number of infected individuals, and R is the number of recovered individuals. β represents the infection rate and γ represents the recovery rate.
The initial conditions for SIR models are determined by the starting values for the number of individuals in each population group. These values can be based on data from previous outbreaks or estimated based on the characteristics of the disease and the population being studied.
SIR models make several assumptions, including a constant population size, a homogeneous population, and a constant infection rate. These assumptions may not always hold true in real-world situations, but they provide a simplified framework for studying disease spread and making predictions.
SIR model predictions can be improved by incorporating more data and adjusting the model parameters based on new information. This can include factors like changes in behavior, vaccination rates, and the emergence of new strains of a disease. Additionally, more complex models that incorporate additional variables can provide more accurate predictions but may require more data and computing power.