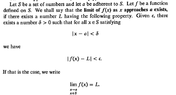- #1
rudransh verma
Gold Member
- 1,067
- 95
- TL;DR Summary
- What is the change actually at some time ##t_0##?
We define differentiation as the limit of ##\frac{f(x+h)-f(x)}h## as ##h->0##. We find the instantaneous velocity at some time ##t_0## using differentiation and call it change at ##t_0##. We show tangent on the graph of the function at ##t_0##. But after taking h or time interval as zero to find the instantaneous change there is no two points left for change to occur. Change at ##t_0## is meaningless in the same way as the slope at a point. How can there be a change at say 5 sec? We have to take two points to talk about change in between them.