HP 50g calculator's answer is correct or author's answer is correct?

[WMDhamnekar]

Summary: Evaluate $\displaystyle\iint\limits_R e^{\frac{x-y}{x+y}} dA$ where $R {(x,y): x \geq 0, y \geq 0, x+y \leq 1}$

Author has given the answer to this question as $\frac{e^2 -1}{4e} =0.587600596824$ But hp 50g pc emulator gave the answer after more than 11 minutes of time 1.11888345561.

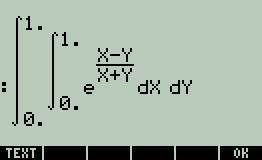
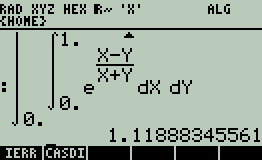
Author's answer

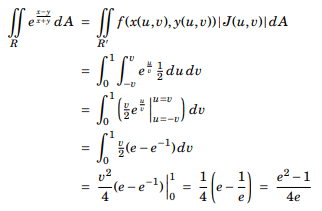Now, How to decide which answer is correct?

 

[Mark44]

Your limits of integration are wrong on the inner integral. The integral you entered into the simulator has the region R being $\{(x, y) | 0 \le x \le 1, 0 \le y \le 1 \}$. IOW, the square bounded by the lines x = 0, y = 0, x = 1, and y = 1. This is incorrect, since the region of integration is a triangle.

Integrating with respect to y first, your integral should look like this:
$$\int_{x=0}^1\int_{y=0}^{1 - x} e^{\frac{x-y}{x+y}}dy dx$$