Huygens' Principle: Exploring a Single Slit Experiment

In summary, the Huygens slit experiment shows that when a wave enters a slit, it forms a number of point sources due to the wave's ability to create new waves in all directions. The diagram attached shows 6 point sources, but this number is arbitrarily chosen and in reality, every point in the slit sends out a wave.
  • #1
Toby_Obie
19
0
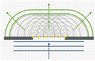
Hello , as per diagram (attached) regarding Huygens slit experiment / diagram

When the wave enters the slit - why does it form a number of point sources ?

There are 6 as per the diagram, Are these the horizontal wavelengths of the electromagnetic waves ?

Thanks, much appreciated
 

Attachments

  • Slit.JPG
    Slit.JPG
    27.6 KB · Views: 430
Physics news on Phys.org
  • #2
The "why" part is pretty easy to understand intuitively if you think about waves on a pond. These waves are created when something disturbs the water's surface--that is, something moves the water up or down. A wave moves water up and down, so the wave itself creates waves that spread out in all directions. In other words, every point inside the wavefront is creating new waves.

6 was as arbitrarily chosen number. In reality, every point in the slit sends out a wave.
 

FAQ: Huygens' Principle: Exploring a Single Slit Experiment

1. What is Huygens' Principle?

Huygens' Principle is a theory proposed by Dutch scientist Christiaan Huygens in the 17th century, which states that every point on a wavefront acts as a source of secondary spherical waves, and the sum of these secondary waves determines the direction of propagation of the wave.

2. How does Huygens' Principle explain the behavior of light in a single slit experiment?

In a single slit experiment, light waves pass through a narrow slit and diffract, creating a pattern of light and dark fringes on a screen. Huygens' Principle explains this behavior by stating that each point on the slit acts as a source of secondary waves, which interfere with each other and create the diffraction pattern on the screen.

3. What is the significance of Huygens' Principle in understanding the nature of light?

Huygens' Principle played a crucial role in understanding the wave nature of light. Before its proposal, light was thought to travel in straight lines, but Huygens' Principle showed that light behaves like a wave, and can undergo diffraction, interference, and refraction.

4. Are there any limitations to Huygens' Principle?

Yes, Huygens' Principle has its limitations. It cannot fully explain the behavior of light in all situations, such as in the presence of obstacles or in materials with varying refractive indices. Other theories, such as the wave theory of light, are needed to fully understand the nature of light.

5. How has Huygens' Principle been further developed and applied in modern science?

Huygens' Principle has been further developed and applied in various fields of science, including optics, acoustics, and quantum mechanics. It has been used to explain phenomena such as diffraction, scattering, and the behavior of waves in different mediums. It has also been applied in technologies such as holography and radar systems.

Similar threads

I Calculating Intensity in Single Slit Diffraction Experiments
Replies
17
Views
2K
Derivation of single slit diffraction formula
Replies
9
Views
2K
Young's double slit experiment green laser
Replies
2
Views
2K
Thomas Young's double slit experiment
Replies
6
Views
4K
B Explanation for bright fringes in Single Slit Diffraction
Replies
4
Views
839
Diffraction through a single slit
Replies
2
Views
2K
Intensity for Young’s Double Slit Interference
Replies
9
Views
5K
I Is the uncertainty principle applicable to single slit diffraction?
Replies
2
Views
789
I Does two-slit sound-wave interference pattern return to original form?
Replies
10
Views
1K
Wavelength of Sound: Solve Using X & Y
Replies
6
Views
1K

Hot Threads

Recent Insights

Back
Top