ker mod
- 4
- 0
Hello,
A friend of mine challenged me with a question related to erection of missile launcher. For some reason and after too long struggling with it i gave up and trying now to figure out what is the point that I'm missing. The task is to fine the force that the piston is "feeling" as function of the angle of the launcher. I have attached a picture. Can someone provide me an elaborated solution?
In addition, i would like to have a graph of this relation between force and angle?
I got lost with the trigonometry...
Keril
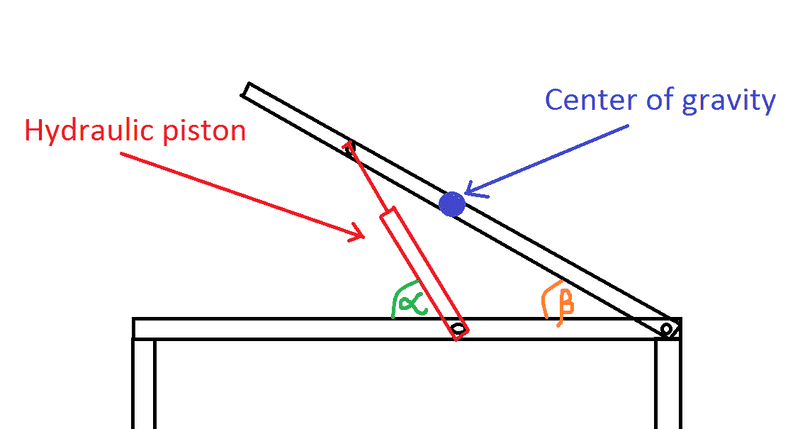
A friend of mine challenged me with a question related to erection of missile launcher. For some reason and after too long struggling with it i gave up and trying now to figure out what is the point that I'm missing. The task is to fine the force that the piston is "feeling" as function of the angle of the launcher. I have attached a picture. Can someone provide me an elaborated solution?
In addition, i would like to have a graph of this relation between force and angle?
I got lost with the trigonometry...
Keril
