abuh11
- 12
- 0
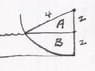
No template because of misplaced homework
Hi, i would like to know how to do this question for fluid mechanics. Sorry as I am new i didnt know how to upload images so i just uploaded the image in justpaste, here is the link http://justpaste.it/pz7r