Hydrostatic Pressure Sluice Gate - Civil Engineering

[JimCrown]

Homework Statement

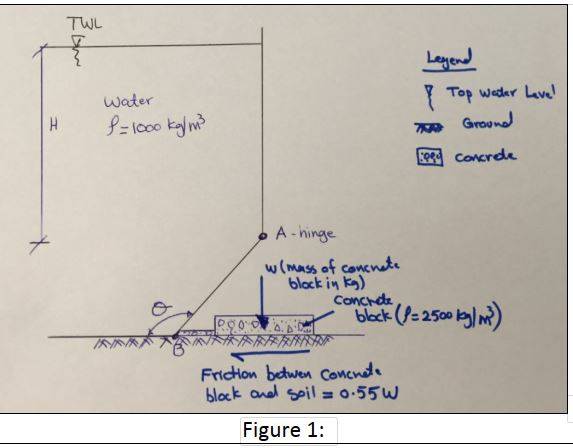
Calculate the concrete volume that is required to keep the sluice gate AB closed, assuming that the only resisting force is the friction between the concrete block and soil. The sluice door is square (900 x 900 mm) and hinged at point A (refer to Figure 1).

Use a factor of safety of 1.5.

Take density of water 1000 kg/m3 and concrete 2500 kg/m3. Assume the friction between the concrete block and soil is 0.55 x concrete mass

Height/H = 5.4m

Degree = 140

Relevant Equations

My working out is:

Sine 140 = AC/0.9 AC = 0.9*sin40 = 0.579m

y = 5.4 + (0.579/2) = 5.6895

A = 0.9*0.9 = 0.81m^2

R = pgyA = 1000*9.81*0.81*5.6895 = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413

IGG = bd^3 / 12 = 0.9*0.9^3 / 12 = 0.0547m^4

D/Magnitude = 0.413 (0.0547 + 0.081(5.6895/0.643)^2 / 0.81*5.6895) = 5.688m


I am now perplexed an confused on how to find the volume of concrete to keep the gate shut.

Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688 - 5.1105 / sin140 = 0.5775m

EA (Middle of gate) = 0.9/2 = 0.45

45.2093*(0.5775 + 0.45) = W*0.55

W = 84.459 KN x (1000/9.81) = 8609.5 kg

I do not know how to get the concrete volume and how will I use the factor of safety

Please can you help with a question I am struggling with. I have done as much working out as I could until I was completely stumped:

Calculate the concrete volume that is required to keep the sluice gate AB closed, assuming that the only resisting force is the friction between the concrete block and soil. The sluice door is square (900 x 900 mm) and hinged at point A (refer to Figure 1).

Use a factor of safety of 1.5.

Take density of water 1000 kg/m3 and concrete 2500 kg/m3. Assume the friction between the concrete block and soil is 0.55 x concrete mass

Height/H = 5.4m

Degree = 140

I have tried again and got this

My working out is:

Sine 140 = AC/0.9 AC = 0.9*sin40 = 0.579m

y = 5.4 + (0.579/2) = 5.6895

A = 0.9*0.9 = 0.81m^2

R = pgyA = 1000*9.81*0.81*5.6895 = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413

IGG = bd^3 / 12 = 0.9*0.9^3 / 12 = 0.0547m^4

D/Magnitude = 0.413 (0.0547 + 0.081(5.6895/0.643)^2 / 0.81*5.6895) = 5.688m


I am now perplexed an confused on how to find the volume of concrete to keep the gate shut.

Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688 - 5.1105 / sin140 = 0.5775m

EA (Middle of gate) = 0.9/2 = 0.45

45.2093*(0.5775 + 0.45) = W*0.55

W = 84.459 KN x (1000/9.81) = 8609.5 kg

I do not know how to get the concrete volume and how will I use the factor of safety

 

[hutchphd]

If you know the mass of concrete, they give you the density. Therefore you can find the volume.
There are several errors in your calculation: always carry the units and carefully cancel them to assure correctness. Get in that habit starting now...please redo.

 

[JimCrown]

I have tried again. The only error I found was the D-y value from a previous attempt I forgot to replace the old y value with the new y value. How is this?


Sine 140 = AC/0.9 AC = 0.9*sin140 = 0.579m

y = 5.4 + (0.579/2) = 5.6895

A = 0.9*0.9 = 0.81m^2

R = pgyA = 1000*9.81*0.81*5.6895 = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413

IGG = bd^3 / 12 = 0.9*0.9^3 / 12 = 0.0547m^4

D/Magnitude = 0.413 (0.0547 + 0.081(5.6895/0.643)^2 / 0.81*5.6895) = 5.688m



Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688 - 5.6895/ sin140 = -0.00233358574m

EA (Middle of gate) = 0.9/2 = 0.45

45.2093*(-0.00233358574 + 0.45) = W*0.55

W = 36.798 KN * (1000/9.81) = 3751.07 kg

Convert weight into mass

Mass = 3751.07* 9.81 = 36798

Volume of Concrete = Mass/Density = 36798/2500 = 14.72

 

[hutchphd]

Please include units in every calculation. Every term in every entry. You have still made multiple errors and I personally am not going to chase them down.

 

[JimCrown]

I don't see any more errors after following the formulas I was given. I know you have just stated you will not point them out but, I have been trying and trying and cannot see them. It is not like I have just posted the question with no serious attempt at attempting or answering it. I was missing putting metres down for some measurements (the answers) and then putting the volume of concrete as m^3 at the end (I don't put the measurements for units in the sums I do). I am sorry if I offended you, I was only asking for help as I did not know how to do the final stages of the question. If you can help it would be greatly appreciated as I am struggling after trying to grasp more knowledge from additional textbooks.

This is the problem with the units for all the answers:

Sine 140 = AC/0.9 AC = 0.9*sin140 = 0.579m

y = 5.4 + (0.579/2) = 5.6895m

A = 0.9*0.9 = 0.81m^2

R = pgyA = 1000*9.81*0.81*5.6895 = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413m

IGG = bd^3 / 12 = 0.9*0.9^3 / 12 = 0.0547m^4

D/Magnitude = 0.413 (0.0547 + 0.081(5.6895/0.643)^2 / 0.81*5.6895) = 5.688m



Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688 - 5.6895/ sin140 = -0.00233358574m

EA (Middle of gate) = 0.9/2 = 0.45m

45.2093*(-0.00233358574 + 0.45) = W*0.55

W = 36.798 KN * (1000/9.81) = 3751.07 kg

Here I think I am going wrong. Do I just multiply the 3751.07 by 0.55 then divide by the density of the concrete (2500) to get the volume?

Convert weight into mass

Mass = 3751.07* 9.81 = 36798 kg

Volume of Concrete = Mass/Density = 36798/2500 = 14.72 m^3

 

[hutchphd]

every number has units. write each of them down. you will discover your mistake...if not I will gladly look at the effort

 

[JimCrown]

900mm = 0.9m

Sine 140 = AC/0.9m AC = 0.9m*sin140 = 0.579m

y = 5.4m + (0.579m/2) = 5.6895m

A = 0.9m*0.9m= 0.81m^2

R = pgyA = 1000 kg/m^3*9.81m/s*0.81m^2*5.6895m = 45209.3 N = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413m

IGG = bd^3 / 12 = 0.9m*0.9m^3 / 12 = 0.0547m^4

D/Magnitude = 0.413m (0.0547m^4 + 0.081m^2(5.6895m/0.643m)^2 / 0.81m^2*5.6895m) = 5.688m



Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688m - 5.6895m / sin140 = -0.00233358574m

EA (Middle of gate) = 0.9m/2 = 0.45m

45.2093 KN*(-0.00233358574m + 0.45m) = W*0.55

W = 36.798 KN * (1000kg/m^3 / 9.81m/s) = 3751.07 kg

All these units above are done and everything seems fine as I have followed the formulas I was given.

The errors I assume are here:

Here I think I am going wrong. Do I just multiply the 3751.07 kg by 0.55 then divide by the density of the concrete (2500 kg/m^3) to get the volume?

I have done changes here:

Volume of Concrete = Mass/Density = 3751.07kg / 2500 kg/m^3 = 1.5 m^3

 

[Tom.G]

What are the units on each side of the "=" for this?
sin140^2 = 0.413m

 

[JimCrown]

Sorry if it was not clear:

sin140 degrees (140°)
140^2 is 140 squared
0.413 metres

 

[Tom.G]

What is the value of sin(140)?
You have not specified a unit of that. What is the unit of sin(140)?

 

[JimCrown]

Sorry for that again. sin140 is 0.643 to 3dp

 

[Tom.G]

OK, our calculators agree on 0.643.

Now answer the other question I asked!
What are the units of 0.643?
And what are the units of 0.643²?

 

[JimCrown]

Sorry, I believe that Sine function has no units as it is ratio of lengths. It is known to be sin θ

As sin is defined as the ratio between the opposite leg and the hypotenuse, its dimension is length / length =1 (i.e. it is dimensionless).

 

[Tom.G]

Correct.

Then why is there a unit assigned to the right side of:

sin140^2 = 0.413m

 

[JimCrown]

Sorry my mistake that should be unitless then

 

[Tom.G]

Correct.

Now you may be able to find the way to your problem solution.
I will now retire (bed time here) and return this thread to you and @hutchphd.

Cheers,
Tom

 

[JimCrown]

Even without the metres I am still getting the same answer which, I do not think is correct


900mm = 0.9m

Sine 140 = AC/0.9m AC = 0.9m*sin140 = 0.579m

y = 5.4m + (0.579m/2) = 5.6895m

A = 0.9m*0.9m= 0.81m^2

R = pgyA = 1000 kg/m^3*9.81m/s*0.81m^2*5.6895m = 45209.3 N = 45.2093 kN

D/Magnitude = sin^2 (IGG + A (y/sin)^2 / A *y)

sin140^2 = 0.413

IGG = bd^3 / 12 = 0.9m*0.9m^3 / 12 = 0.0547m^4

D/Magnitude = 0.413 (0.0547m^4 + 0.081m^2(5.6895m/0.643)^2 / 0.81m^2*5.6895m) = 5.688m



Would it be:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688m - 5.6895m / sin140 = -0.00233358574m

EA (Middle of gate) = 0.9m/2 = 0.45m

45.2093 KN*(-0.00233358574m + 0.45m) = W*0.55

W = 36.798 KN * (1000kg/m^3 / 9.81m/s) = 3751.07 kg

All these units above are done and everything seems fine as I have followed the formulas I was given.

The errors I assume are here:

Here I think I am going wrong. Do I just multiply the 3751.07 kg by 0.55 then divide by the density of the concrete (2500 kg/m^3) to get the volume?

I have done changes here:

Volume of Concrete = Mass/Density = 3751.07kg / 2500 kg/m^3 = 1.5 m^3

 

[hutchphd]

This makes no sense:

Sine 140 = AC/0.9m AC = 0.9m*sin140 = 0.579m

Put units in for Newtons (kgm/s²) and see if this is incorrect

W = 36.798 KN * (1000kg/m^3 / 9.81m/s) = 3751.07 kg

When I suggest putting units in, the purpose is to compare each term and see that it makes sense (one cannot add meters to seconds...). So you need to redo this calculation and check each line as it is written for dimensional consistency by reducing to similar units (time length and mass are most usual) . Like the lines above And you need to get in that habit every time you calculate (or do algebra). This is like practicing scales on a piano...soon you will do it automatically and it makes life much easier.

Also the symbol for kilo is always k not K...

 

[JimCrown]

Sorry if it is unclear:

Sine 140 = AC/0.9m AC = 0.9m*sin140 = 0.579m

This is sin140 = AC / 0.9m

So I rearranged the equation so AC becomes the subject so it becomes AC = 0.9m * sin140 = 0.579m


I divided it by (1000 / 9.81) to convert the kN into kg

Then, I could find the volume as I had the mass and density figures.

I am not sure if this is correct though? As I believe everything is correct until I reach:

R*(FE + EA) = W*0.55

sin140 = D - y / EF EF = D - y / sin140 = 5.688m - 5.6895m / sin140 = -0.00233358574m

EA (Middle of gate) = 0.9m/2 = 0.45m

45.2093 KN*(-0.00233358574m + 0.45m) = W*0.55

W = 36.798 KN * (1000kg/m^3 / 9.81m/s) = 3751.07 kg

All these units above are done and everything seems fine as I have followed the formulas I was given.

The errors I assume are here:

Here I think I am going wrong. Do I just multiply the 3751.07 kg by 0.55 then divide by the density of the concrete (2500 kg/m^3) to get the volume?

I have done changes here:

Volume of Concrete = Mass/Density = 3751.07kg / 2500 kg/m^3 = 1.5 m^3

 

[hutchphd]

R*(FE + EA) = W*0.55

units check? every term every time

If the units are inconsistent then the equation is certainly incorrect.
How did you get this?

 

[JimCrown]

That is part of the formula I was given.

R is the Force:

R = pgyA = 1000*9.81*0.81*5.6895 = 45.2093 kN

I meant to put EF as FE. And EA is the middle of the gate. The units are fine after checking through everything and so are the sums until a certain point when I do not know what I am doing.

 

[hutchphd]

Describe your approach in maybe five steps and indicate where it goes off the rails (and what you don't understand). I think at the point in question you are equatinq torgue to Force...no can do..

 

[JimCrown]

The first calculations are all correct and follow the formula I was given. I am having trouble when I reach here (mainly how to find out the volume of concrete) I believe it to be 1.5 m^3

I am not equating torque with force I just think we are having a serious miscommunication:


I am not sure if this is correct though? As I believe everything is correct until I reach:

R*(FE + EA) = W*0.55

sin140 = D - y / FE

FE = D - y / sin140 = 5.688m

5.688m - 5.6895m / sin140 = -0.00233358574m

EA (Middle of gate) = 0.9m/2 = 0.45m

45.2093 KN*(-0.00233358574m + 0.45m) = W*0.55

W = 36.798 KN * (1000kg/m^3 / 9.81m/s) = 3751.07 kg

All these units above are done and everything seems fine as I have followed the formulas I was given.

The errors I assume are here:

Here I think I am going wrong. Do I just multiply the 3751.07 kg by 0.55 then divide by the density of the concrete (2500 kg/m^3) to get the volume?

I have done changes here:

Volume of Concrete = Mass/Density = 3751.07kg / 2500 kg/m^3 = 1.5 m^3