- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Hydrostatics: long, bent tube
- Thread starter dk_ch
- Start date
-
- Tags
- Hydrostatics Tube
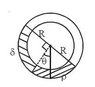
In summary, the conversation is about finding the angle θ in a problem involving a uniform long tube bent into a circle and filled with two liquids of different densities. The conversation includes discussing the condition for hydrostatic equilibrium, using trigonometry to solve the problem, and drawing a figure to visualize the problem. The final solution involves finding the vertical and horizontal distances of the liquids and relating them to the angle θ. The approach suggested by the expert involves finding the vertical height of the heavy liquid and using its difference in height with the light liquid to solve for θ.
Physics news on Phys.org
- #2
NascentOxygen
Staff Emeritus
Science Advisor
- 9,242
- 1,074
How would you approach a problem like this?
- #3
dk_ch
- 44
- 0
NascentOxygen said:How would you approach a problem like this?
I tried taking length of equal arcs of two diff liquid col of same volume as "l" and arc length corresponding to angle θ as x and equating masses of liq columns of both sides of vertical line I got
x/(l-x) =(ρ-δ)/(ρ+δ)
if it is correct what to do next ?
- #4
- 21,512
- 12,673
What is the condition for hydrostatic equilibrium? Is it that the masses on both sides are equal or is it something else?
- #5
dk_ch
- 44
- 0
Orodruin said:What is the condition for hydrostatic equilibrium? Is it that the masses on both sides are equal or is it something else?
In hydrostatic equilibrium the pressures must be equal .we are to measure pressures which depend on height. How can height be measured in terms of R and θ?
- #6
- 21,512
- 12,673
Correct, pressure = height x density.
It is now time to do your trigonometry homework
It is now time to do your trigonometry homework
- #7
dk_ch
- 44
- 0
Orodruin said:Correct, pressure = height x density.
It is now time to do your trigonometry homework
please help to solve it.
- #8
- 21,512
- 12,673
I can try to guide you, but I will not solve he problem for you as per forum rules (which are reasonable in order to encourage you to think).
Well, to start you know the geometry of the problem. Each fluid takes up a full right angle in the pipe. I would start by drawing circles and triangles and try to relate the height of the right column in the figure to the angle θ. Then continue by finding the height of the heavy liquid on the left side and last the height of the light liquid. It will also help to draw a horizontal and a vertical line through the center of the circle.
Well, to start you know the geometry of the problem. Each fluid takes up a full right angle in the pipe. I would start by drawing circles and triangles and try to relate the height of the right column in the figure to the angle θ. Then continue by finding the height of the heavy liquid on the left side and last the height of the light liquid. It will also help to draw a horizontal and a vertical line through the center of the circle.
- #9
dk_ch
- 44
- 0
orodruin said:i can try to guide you, but i will not solve he problem for you as per forum rules (which are reasonable in order to encourage you to think).
Well, to start you know the geometry of the problem. Each fluid takes up a full right angle in the pipe. I would start by drawing circles and triangles and try to relate the height of the right column in the figure to the angle θ. Then continue by finding the height of the heavy liquid on the left side and last the height of the light liquid. It will also help to draw a horizontal and a vertical line through the center of the circle.
please draw the fig and show the heights
- #10
- 21,512
- 12,673
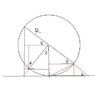
You already have a figure that you attached to your first post. I suggest you start from there and draw the vertical distance from the bottom to the surface of one of the liquids. I would like to help you, but you have to show some effort and make an attempt, after that I can tell you whether it is right and point you in the right direction if it is not.
- #11
dk_ch
- 44
- 0
Orodruin said:You already have a figure that you attached to your first post. I suggest you start from there and draw the vertical distance from the bottom to the surface of one of the liquids. I would like to help you, but you have to show some effort and make an attempt, after that I can tell you whether it is right and point you in the right direction if it is not.
Here is the construction. where I get vertical length of lighter liq col at left = Rcos θ +Rsin θ
horizontal length of denser liq col at left = Rsin θ
horizontal length of denser liq col at right =Rcos θ
then shall i take total length of horizontal liq col ?
this can give the result . but height should be vertical. Is the proceeding correct?
Attachments
Last edited:
- #12
- 21,512
- 12,673
Very good. Yes, you must find the verical height of the heavy liquid.
So now it is a matter of finding the heights above the bottom of the heavy liquid. Let us start with the right side, the vertical line through the center of the circle has length R. It must be equal to the height of the fluid on that side plus the height of one of the triangles. Which triangle and what is the height of that triangle expressed in R and θ?
So now it is a matter of finding the heights above the bottom of the heavy liquid. Let us start with the right side, the vertical line through the center of the circle has length R. It must be equal to the height of the fluid on that side plus the height of one of the triangles. Which triangle and what is the height of that triangle expressed in R and θ?
- #13
dk_ch
- 44
- 0
Orodruin said:Very good. Yes, you must find the verical height of the heavy liquid.
So now it is a matter of finding the heights above the bottom of the heavy liquid. Let us start with the right side, the vertical line through the center of the circle has length R. It must be equal to the height of the fluid on that side plus the height of one of the triangles. Which triangle and what is the height of that triangle expressed in R and θ?
If the vertical ht of denser liq at left be taken as Rsinθ and at right as Rcosθ then result will come. but how is it possible
If the difference of vertical ht between rt and left of denser liq is taken as the resultant ht( ie Rcos θ -Rsin θ ) balancing the the vertical ht of lighter liq of ht Rcos θ +Rsin θ ,ht measured from the junction of the two liquids then the it will satisfy the result.
I think that I have done right thing.
please comment
Last edited:
- #14
- 21,512
- 12,673
Because this gives the same difference between the heights as computing the actual heights. This is also a valid way of making the computation. The difference in height of the heavy liquid times ρ has to equal the height of the light liquid times δ. The reason it gives the same difference is related to a 90 degree rotation.
Let us try the following: You know the distance from thte bottom to the center of the circle. You have obviously managed to compute the horizontal distance from the light-heavy interface to the horizontal line through the center of the circle. What is then the height of the heavy liquid to the left? A similar argument can be made on the right side.
Let us try the following: You know the distance from thte bottom to the center of the circle. You have obviously managed to compute the horizontal distance from the light-heavy interface to the horizontal line through the center of the circle. What is then the height of the heavy liquid to the left? A similar argument can be made on the right side.
- #15
dk_ch
- 44
- 0
Orodruin said:Because this gives the same difference between the heights as computing the actual heights. This is also a valid way of making the computation. The difference in height of the heavy liquid times ρ has to equal the height of the light liquid times δ. The reason it gives the same difference is related to a 90 degree rotation.
Let us try the following: You know the distance from thte bottom to the center of the circle. You have obviously managed to compute the horizontal distance from the light-heavy interface to the horizontal line through the center of the circle. What is then the height of the heavy liquid to the left? A similar argument can be made on the right side.
thanks for encouraging ,
1. What is hydrostatics?
Hydrostatics is the study of fluids at rest, specifically focusing on the pressure exerted by fluids and how it affects bodies immersed in them.
2. What is a long, bent tube used for in hydrostatics?
A long, bent tube is commonly used to demonstrate the principles of hydrostatics, such as Pascal's law and the concept of pressure changes in a fluid.
3. How does a long, bent tube work in demonstrating hydrostatics?
The long, bent tube is filled with a fluid, often water, and then bent to different angles. The pressure at each point in the tube can be measured and compared, demonstrating the effects of gravity and fluid pressure.
4. What are some real-world applications of hydrostatics using a long, bent tube?
One example of a real-world application of a long, bent tube in hydrostatics is in hydraulic systems, where the principles of pressure and fluid flow are used to power machines and equipment.
5. Is a long, bent tube the only way to demonstrate hydrostatics?
No, there are other methods and devices that can be used to demonstrate the principles of hydrostatics, such as the use of different types of containers and pumps.
Similar threads
-
Introductory Physics Homework Help
- Replies
- 2
- Views
- 667
-
Introductory Physics Homework Help
- Replies
- 6
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 1
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 29
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 10
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 6
- Views
- 6K
-
Introductory Physics Homework Help
- Replies
- 10
- Views
- 7K
- Replies
- 40
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 6
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 14
- Views
- 1K
Share: