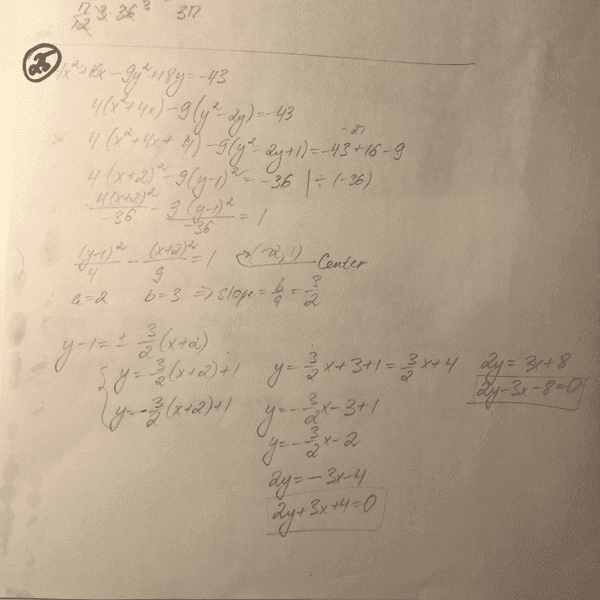The discussion revolves around the confusion regarding the slopes of hyperbola asymptotes, specifically whether the correct slope is a/b or b/a. Participants clarify that the slope of the asymptote can be derived from the general equation of a hyperbola, leading to the conclusion that the slope is indeed a/b, resulting in a factor of 2/3. A method for calculating the slope using conic section coefficients is also shared, confirming that the slope in this case is -2/3. Additionally, advice is given to avoid posting images of work, as it may hinder assistance from others. The conversation emphasizes the importance of understanding the derivation of formulas for clarity.