- #1
Zahid Iftikhar
- 121
- 24
Please help in the explanation of BH curve (See attached file).
At the starting point, more current is required to bring the material to its magnetic saturation point( in fig form origin to pt.a shown by purple line ) as compared to when the material is fully demagnetized and then brought to same saturation point (in fig from point d to point a, shown by green line). At the origin and point d of the graph the material is totally demagnetized with B=0, then different current is required to reach the saturation point?
Regards
Zahid
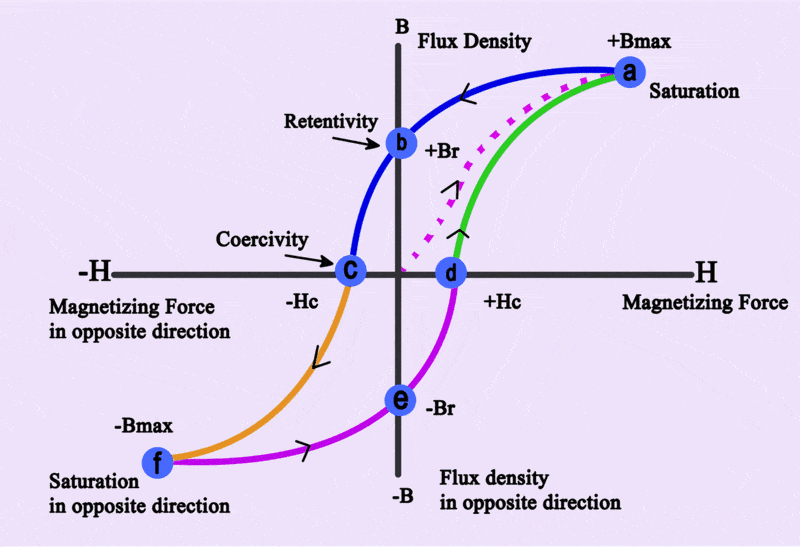
At the starting point, more current is required to bring the material to its magnetic saturation point( in fig form origin to pt.a shown by purple line ) as compared to when the material is fully demagnetized and then brought to same saturation point (in fig from point d to point a, shown by green line). At the origin and point d of the graph the material is totally demagnetized with B=0, then different current is required to reach the saturation point?
Regards
Zahid



