Ideal gas undergoes cycle process

AI Thread Summary
The discussion centers on the behavior of an ideal gas undergoing a cyclic process as represented in a PV graph. The upper graph shows linear relationships between temperature and pressure, indicating constant volume, which results in vertical lines in the PV graph. In contrast, the lower graph does not maintain these relationships, leading to confusion about its validity. The ideal gas law, pV = nRT, supports the conclusions drawn from the upper graph. Understanding these relationships is crucial for accurately interpreting the gas's behavior in the cycle process.
b_andries
Messages
13
Reaction score
0
Hi,

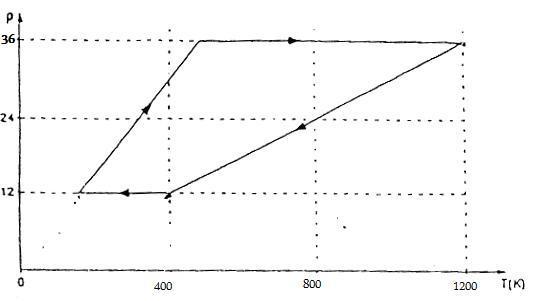
An amount of ideal gas undergoes the folowing cycle process in the following graph:

attachment.php?attachmentid=33655&stc=1&d=1301348391.jpg


This process can be presented by the following PV-graph :
attachment.php?attachmentid=33656&stc=1&d=1301348391.jpg


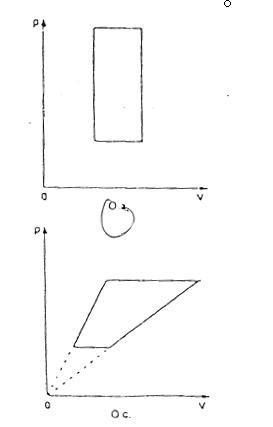
The answer has to be the upper graph but why can't it be the lower graph ?
Thank you!
 

Attachments

  • cycle process.jpg
    cycle process.jpg
    13.1 KB · Views: 530
  • grafiek.jpg
    grafiek.jpg
    5.8 KB · Views: 601
Physics news on Phys.org
An ideal gas has: p V = n R T

That is: V = n R T / p

As you can see in the upper graph there are linear relations between T and p, meaning V must be constant, resulting in vertical lines in the p-V-graph.
Note that the diagonal lines in the upper graph can be extended to intersect the axes at the origin.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Why is temperature constant after gas has expanded?
Replies
33
Views
2K
Internal Energy of an Ideal Gas
Replies
4
Views
2K
Closed cycle of an ideal gas
Replies
3
Views
1K
Thermodynamics: Two gases in a container
Replies
1
Views
564
PV Diagram of Ideal Monatomic Gas Processes
Replies
4
Views
2K
Pressure Volume graph finding total mole of gas
Replies
6
Views
4K
Thermodynamics: Ideal gas model
Replies
1
Views
1K
Why must we use absolute temperature for the Ideal Gas Law?
Replies
10
Views
3K
Is My Solution for Part D Logically Correct?
Replies
7
Views
2K
Efficiency of Stirling Cycle - Is it the same as the Carnot Engine?
Replies
14
Views
1K

Hot Threads

Recent Insights

Back
Top