Ertosthnes
- 49
- 0
I worked this problem out, but my numbers make me think that my solution is wrong. Can you check this for me?
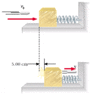
A 5.00 g bullet moving with an initial speed of v0 = 420 m/s is fired into and passes through a 1.00 kg block. The block, initially at rest on a frictionless horizontal surface, is connected to a spring with a spring constant of 950 N/m.
(a) If the block moves 5.00 cm to the right after impact, find the speed at which the bullet emerges from the block.
(b) If the block moves 5.00 cm to the right after impact, find the mechanical energy lost in the collision.

My attempt at a solution
a) P(o) = P(f)
m(1)v(1) + m(2)v(2) = (m(1) + m(2))*v(f)
^This is to find the velocity of the bullet and the block while the bullet is in the block - I'm thinking that it neglects the fact that the block has to accelerate, and that the spring is pushing back on the block. Anyway...
v(f) = 2.09 m/s
Then, to find the speed of the bullet when it exits the block:
m(1)v(1) + m(2)v(2) = m(1)v(1) + m(2)v(2)
Letting m(1) be the bullet, and m(2) be the block, v(2) = 2 m/s? Seems too slow.
b) E(o) = E(f)
m(1)v(1)^2 + m(2)v(2)^2 + kx(o)^2 = m(1)v(1)^2 + m(2)v(2)^2 + kx(f)^2
^The reason you don't see any (1/2)'s is because they all had (1/2)'s, so I multiplied the whole thing by 2.
882 = 6.76
Difference in mechanical energy = 882 - 6.76 = 875.2 J lost?
Where'd all the energy go, anyway? Was it absorbed by the spring?
A 5.00 g bullet moving with an initial speed of v0 = 420 m/s is fired into and passes through a 1.00 kg block. The block, initially at rest on a frictionless horizontal surface, is connected to a spring with a spring constant of 950 N/m.
(a) If the block moves 5.00 cm to the right after impact, find the speed at which the bullet emerges from the block.
(b) If the block moves 5.00 cm to the right after impact, find the mechanical energy lost in the collision.
My attempt at a solution
a) P(o) = P(f)
m(1)v(1) + m(2)v(2) = (m(1) + m(2))*v(f)
^This is to find the velocity of the bullet and the block while the bullet is in the block - I'm thinking that it neglects the fact that the block has to accelerate, and that the spring is pushing back on the block. Anyway...
v(f) = 2.09 m/s
Then, to find the speed of the bullet when it exits the block:
m(1)v(1) + m(2)v(2) = m(1)v(1) + m(2)v(2)
Letting m(1) be the bullet, and m(2) be the block, v(2) = 2 m/s? Seems too slow.
b) E(o) = E(f)
m(1)v(1)^2 + m(2)v(2)^2 + kx(o)^2 = m(1)v(1)^2 + m(2)v(2)^2 + kx(f)^2
^The reason you don't see any (1/2)'s is because they all had (1/2)'s, so I multiplied the whole thing by 2.
882 = 6.76
Difference in mechanical energy = 882 - 6.76 = 875.2 J lost?
Where'd all the energy go, anyway? Was it absorbed by the spring?