Identifying Forces and Directions in Torque and Equilibrium

In summary, a person is seeking help with understanding torque and drawing a free body diagram for a tripod. The first two questions involve finding the forces and their directions for each leg of the tripod in order to support one third of the object's weight. They are still struggling to understand and are asking for further assistance.
  • #1
Intr3pid
39
0
hello everyone

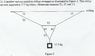
I recently started learning about torque and I'm having a lot of trouble with the first 2 questions. Can someone help me out with the first two questions?

btw, I don't quite understand how to draw the free body diagram for the first question.

PS the questions are located on the attachments
 

Attachments

  • tripod.JPG
    tripod.JPG
    45.9 KB · Views: 473
  • equilirbium.JPG
    equilirbium.JPG
    31.8 KB · Views: 453
Last edited:
Physics news on Phys.org
  • #2
Try considering just one 'leg' of the tripod
 
  • #3
can someone help me out please?

I'm really stuck.
 
  • #4
For the first one:
Each leg of the tripod needs to support one third of the object's weight. Keep in mind that this force is being applied strictly vertical
 
  • #5
I still don't quite get it.
 
  • #6
Lets start at the bottom of one leg. What forces do you indentify and in what direction are they?
 

FAQ: Identifying Forces and Directions in Torque and Equilibrium

What is torque?

Torque is a measure of the force that causes an object to rotate around an axis. It is calculated by multiplying the force applied to an object by the distance from the axis of rotation.

How is torque different from force?

Force is a push or pull on an object, while torque is a twisting force that causes an object to rotate. They are related, as torque is the result of a force acting on an object at a distance from the axis of rotation.

What is the unit of measurement for torque?

The unit of measurement for torque is Newton-meters (Nm) in the SI system, or foot-pounds (ft-lb) in the Imperial system.

How does torque affect equilibrium?

For an object to be in equilibrium, the sum of all forces acting on it must be zero, and the sum of all torques acting on it must also be zero. If there is an unbalanced torque, the object will rotate until it reaches a state of equilibrium.

How can torque be increased or decreased?

Torque can be increased by increasing the force applied to an object or by increasing the distance from the axis of rotation. It can be decreased by decreasing the force or the distance from the axis of rotation.

Similar threads

Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board
Replies
6
Views
2K
Torque: find the force necessary for a body to be in equilibrium
Replies
6
Views
2K
Where on a rigid body is a resultant force applied?
Replies
11
Views
743
Calculating Motor Force & Torque
Replies
9
Views
264
Torque on a Pivot Point With Multiple Forces and Different Directions
Replies
6
Views
648
How Do You Calculate Torques for a Ladder in Static Equilibrium?
Replies
2
Views
1K
Solving Equilibrium w/ Plank & Forces | Physics Problem
Replies
7
Views
3K
Calculating torque about a point with given forces
Replies
5
Views
2K
Trouble with Static Equilibrium
Replies
5
Views
2K
Torque and forces (Beginner level)
Replies
14
Views
2K

Hot Threads

Recent Insights

Back
Top