Cody
- 3
- 0
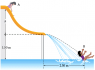
"If the height of the water slide is h = 3.2m and the person's initial speed at point A (at the top of slide) is 0.54m/s, at what location does the swimmer splash down in the pool?"
I saw a thread with the same question back from 2005 but it is now closed.
I understand that you have to use conservation of energy at point A and at the bottom of the slide to find velocity at the bottom of the slide, then use the formula x = v√2y/g.
I am however confused with the following:
Why can I not substitute the exact values for h into the formula i.e
mgh + 1/2 mv^2 = mgh + 1/2 mv^2
since it is known, but rather have to use h-1.50(for the bottom) and 1.50(for the top)
Hope someone understands what I am asking.
Any help is appreciated.
I saw a thread with the same question back from 2005 but it is now closed.
I understand that you have to use conservation of energy at point A and at the bottom of the slide to find velocity at the bottom of the slide, then use the formula x = v√2y/g.
I am however confused with the following:
Why can I not substitute the exact values for h into the formula i.e
mgh + 1/2 mv^2 = mgh + 1/2 mv^2
since it is known, but rather have to use h-1.50(for the bottom) and 1.50(for the top)
Hope someone understands what I am asking.
Any help is appreciated.