I'm having trouble with this proof

[159753x]

I'm having trouble completing this proof for homework.

1. Homework Statement

Prove that cos θ + cos 3θ + cos 5θ + ... + cos (2n-1)θ = (sin 2nθ)/(2 sin θ).
Prove that sin θ + sin 3θ + sin 5θ + ... + sin (2n-1)θ = (sin nθ)^2/(sin θ).

Use Euler's formula and the geometric progression formula.

Homework Equations

Euler's formula is

.
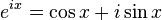The geometric progression formula is

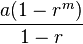, where a is the first term and r is the constant that each term is multiplied by to get the next term.

The Attempt at a Solution

[/B]
I've tried a number of ways, none of which I have been able to simplify. Can anybody who can see the right way to complete this proof perhaps give me some direction? For example, what are the starting points for a and r? I feel like I have tried everything I can think of, but I couldn't simplify it.

How can I do the geometric progression formula if the series isn't exponential? I know I can use Euler's formula to transfer the cosines to exponentials, but how can I do this is the series consists only of cosines? How can I use the formula without the i sin(θ) terms? It seems that I can't substitute for the formula then... Hmm...

If anybody knows any tricks or guidance, it would be greatly appreciated! Thanks in advance

- Leo

 

[Mark44]

I would try mathematical induction.

 

[kreil]

Admittedly I haven't completed the problem before saying this, but my first line of attack would be to use Taylor series expansions for sin and cos.

Hint:
$$e^{ix} = \sum_{n=0}^{\infty} \frac{i^n x^n}{n!} = 1 + ix - \frac{x^2}{2} - i\frac{x^3}{3!} + \frac{x^4}{4!} + i\frac{x^5}{5!} ... = \left(1 - \frac{x^2}{2} + \frac{x^4}{4!} ... \right) + i \left( x-\frac{x^3}{3!} + \frac{x^5}{5!} ... \right)$$

 

[Simon Bridge]

Why not just convert the two series to a sum of exponentials using the Euler formula, then applying the geometric series formula to each?
Alternatively - take the first and add i times the second, so the combined series is now a sum of exponentials, then apply the geometric series formula... simplify and see what falls out.

 

[vela]

Hint: $\cos\theta = \text{real part of }e^{i\theta}$ and $\cos 3\theta = \text{real part of }e^{i3\theta}$, so $\cos \theta + \cos 3\theta = \text{real part of }(e^{i\theta} + e^{3i\theta})$.

 

[159753x]

Thanks to all for the response. I ended up taking the exponential series and dividing it into two parts. One corresponds to e^+iθ and the other corresponds to e^-iθ. I can then easily take these and use the geometric progression formula. At the end of the day, I get REALLY close... I end up getting sin(4n+2)θ / 2 sin θ.

Any way I can simplify this to sin(2nθ) / 2 sin θ?

 

[vela]

Please show your work.

 

[159753x]

Sorry for doing this, but I don't know how to input code on this site. I'll just link to pictures.

Starting with the cosine series, I am able to use this relation: http://i.imgur.com/kUHerIR.png to get this: http://i.imgur.com/PClCbED.png. After simplifying I get the following, which I am certain is correct: http://i.imgur.com/lMk90s8.png.

How do I get rid of that 2n-1 in the numerator? I have the proof down except for that part.

 

[159753x]

EDIT: in the second picture, the exponentials in the denominator should both have θ.

 

[vela]

You need to show more details. Your result is not correct.

You can find a LaTeX FAQ here: https://www.physicsforums.com/threads/physics-forums-faq-and-howto.617567/#post-3977517

 

[159753x]

http://i.imgur.com/MRjOT9K.png

here are the steps of the proof in detail. After the last step, I use the relation: http://i.imgur.com/kUHerIR.png to get to what I mentioned above.