- #1
Nguyen Thanh Nam
- 14
- 0
Can I upload the images here? so that whenever you choose my topic, they're shown, no need for you to open attachments?
Any way, I am a non-native so I get difficulties solving this problem. Tell me! (it's easy but I can't use English to state some sentence)
The URL of the problem:
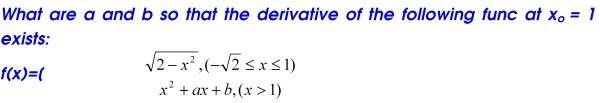
Thanks
Any way, I am a non-native so I get difficulties solving this problem. Tell me! (it's easy but I can't use English to state some sentence)
The URL of the problem:
Thanks