Impedance as seen across two terminals

[anthonych414]

Homework Statement

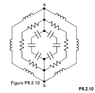
All the inductances in Figure P8.2.10 are j10, all the resistances are 10, and all the capacitances are -j12 . Determine the impedance between terminals 'ab'.

Ans. 27 + j9

Homework Equations

The Attempt at a Solution

I figured I should add up the impedances of the capacitors on the left and divide by 2, doing the same for the inductors and the resistors, then finding the equivalent impedance of the parallel connection of the resistors/inductors/capacitors. I keep getting an answer of 540/37 + 90j/37 Ω. Any idea what I might be doing wrong?

 

[gneill]

Your answer looks correct to me. Maybe they changed component values in the question but didn't update their answer.

 

[ehild]

Your solution looks correct.


ehild