Impedance calculation from base values

[Maverickans]

Hello, I'm reading a paper at the moment and I came across this:

We now apply the solution technique to a single-phase, 3 kW, 240 V ASD heat pump. The ASD has smoothing capacitor C = 4200 pF, (corresponding to approximately 6% ripple in dc voltage), and total impedance (sum of Thevenin and local line) = 8% ∠ 45° (expressed on a base of 240 V, 5 kVA).

Please, could someone help me in finding the actual values of R and L in the circuit attached, with the above values. Also, if possible, is there a way to know the values of Rth, Lth, R1, and L1 individually, with the given information?

Thanks :)

 

[Baluncore]

Please, could someone help me in finding the actual values of R and L in the circuit attached, with the above values. Also, if possible, is there a way to know the values of Rth, Lth, R1, and L1 individually, with the given information?

Welcome to PF.

I believe you can solve for ( Rth + R1 ) and ( Lth + L1 ), but I do not believe you can separate the individual components.

Can you please give us a reference to the paper you are reading.

 

[Maverickans]

Thanks for your reply.

Can you help me solve for ( Rth + R1 ) and ( Lth + L1 ) ?

Here is the reference: https://dokumen.tips/documents/effe...-the-input-current-of-single-phase-diode.html

Thanks once again.

 

[Baluncore]

From a slightly different direction ...
At the end of page 1419 we have;
“The equivalent system impedance of the shared bus is chosen to be (0.4 + j0.25) R, which is representative of a 120 V network [6].”

For a 240 V circuit we might use the same values, (0.4 + j0.25) R, since two lines are being used in both cases.

If we then assume that the fundamental frequency is 60Hz, based on the fact that all the authors are from the USA, we can compute the totals ...
R = 0.4 ohms.
X = 0.25 = 2·π·f·L ;
∴ L = 0.25 / ( 2·π·60 ) ;
∴ L = 0.663 mH.

 

[Maverickans]

Thanks Baluncore, for your clear answer.

Just out of curiosity, how did they calculate the "total impedance (sum of Thevenin and local line) = 8% ∠ 45° (expressed on a base of 240 V, 5 kVA)"

I know Z =U*U/S = 240*240 / 5000 = 11.52 Ohms, but its not in %. And the angle, I'm not sure either.

 

[Baluncore]

OK, so I think I see what is going on here. They are showing that the short conduction angle of the diode bridge, (while it charges the reservoir capacitor), results in a high peak current with harmonic distortion of the current. They then show that because of the impedance of the supply, there will be a drop in line voltage, causing a flat top to the bridge input voltage. That flat top voltage lengthens the conduction angle of the diodes, while the inductance of the supply lines extends the conduction angle further. Their conclusion is that the flat top is an advantage, rather than a disadvantage. (I think this is an excuse for not using a power factor correction circuits, from 25 years ago).

There are two percentages mentioned. Firstly the ripple on the reservoir capacitor. Secondly, the flat top to the voltage profile, with a phase delay due to the line inductance.

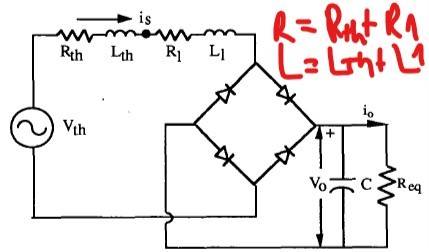
Here is the circuit I used for the simulation.
Single phase 240 Vrms, 3 kW; 60 Hz; Full wave rectifier.
Current; I = 3 kW / 240 V = 12.5 amp.
Work out the load resistor needed. Rload; 240 / 12.5 = 19.2 ohms; = R1.
Peak voltage will be; 240 * √2 = 340 Vdc. (Ignores diode voltage drop).

V(g) is the infinite-bus source, Rsum and Lsum are the total impedance of the local distribution grid.
V(in) is the supply input to the bridge. We can ignore the voltage drop across the conducting diodes.

We can calculate the expected ripple.
Frequency = 60 Hz; Full wave, Period; T = 1 / 120 = 8.333 msec.
By definition; C = Q / V; with Q = I · t.
Ripple amplitude; dv = I · dt / C = 12.5 / (0.0042 * 120 ) = 24.8 volt.
As a percentage; 100 * 24.8 / 340 = 7.3 %.
The period of the rectified AC is 8.333 msec;

Here is the transient response for a single cycle after the circuit has stabilised.

I(Rsum) is the input current. Blue trace. Peak line current is 65 amp. The peak is 670 usec after the peak of V(g). That is 360° * 0.67 / 8.33 = 29°; (Allowing for the 120 Hz).
The green trace is capacitor voltage. It shows 20 volts peak-peak of ripple.
The 24.8 V calculated is close to the simulation. But the calculation did not allow for the reduction due to the flat top.
Notice how V(in) yellow, does not follow V(g) magenta. That is the flat top due to voltage drop on the line. The simulation voltage drop is just under 50 volts.

Notice also that the current continues to flow for some time after V(in) falls below the C1 voltage. That is due to the line inductance, Lsum.

At the moment the diode turns off there is a 150 volt PP transient oscillation at about 6 MHz, which then decays exponentially over about 10 usec. During that period, the diode current is below 2.5 mA, so it is not a problem. It is resonance of the schottky diode off-capacitance with our lump of line inductance. The Q is set by Rsum. In reality it would not be seen as there would be an LC Pi filter on the input, and 6 MHz has a wavelength of about 50 metres. That is a good reason why there needs to be a Pi filter.