knokout5
- 3
- 0
Hello everyone,
This is my first thread so thanks in advance for any help! I have been trying to figure out this problem, and though I've gotten close to an end solution (also with the help of motion analysis on Solidworks) I am not very confident.
So, in order to meet an IEC standard of a mobile cart, I am trying to figure out if a mobile cart can roll over a 10mm step threshold without tipping over going at an initial velocity of 0.8m/s. I have been basically using impulse, momentum, and energy equations from this site:
http://www.real-world-physics-problems.com/impulse-and-momentum.html
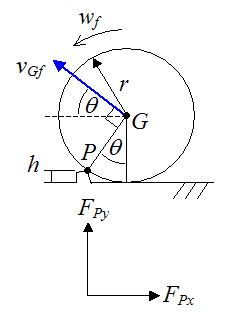
The only tick on my neck is that, all the examples I've found are of one pivot with some moment of inertia of one wheel. In my case, you have TWO pivots:
1) at the center of the wheel, whereabout the center of mass (CM) of the cart is rotating.
2) at the step/wheel contact point.
The wheel will need enough "vertical velocity" to make it over the step, but doesn't that all depend on the force at which the momentum of the CM "pulls" the wheel over the step? My CM is relatively high above the ground, so in my motion analyses I have been seeing the cart tip forward (rear wheels lifted off the floor), and then the wheel rolling over the step, and then the cart come back down. There are two things going on. Any help would be appreciated!
-Mike
This is my first thread so thanks in advance for any help! I have been trying to figure out this problem, and though I've gotten close to an end solution (also with the help of motion analysis on Solidworks) I am not very confident.
So, in order to meet an IEC standard of a mobile cart, I am trying to figure out if a mobile cart can roll over a 10mm step threshold without tipping over going at an initial velocity of 0.8m/s. I have been basically using impulse, momentum, and energy equations from this site:
http://www.real-world-physics-problems.com/impulse-and-momentum.html
The only tick on my neck is that, all the examples I've found are of one pivot with some moment of inertia of one wheel. In my case, you have TWO pivots:
1) at the center of the wheel, whereabout the center of mass (CM) of the cart is rotating.
2) at the step/wheel contact point.
The wheel will need enough "vertical velocity" to make it over the step, but doesn't that all depend on the force at which the momentum of the CM "pulls" the wheel over the step? My CM is relatively high above the ground, so in my motion analyses I have been seeing the cart tip forward (rear wheels lifted off the floor), and then the wheel rolling over the step, and then the cart come back down. There are two things going on. Any help would be appreciated!
-Mike
Last edited:
