How Is Force Calculated to Keep a Block Stationary on an Inclined Plane?

[bjgawp]

Homework Statement

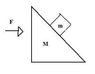
A small block of mass m rests on the sloping side of a triangular block of mass M which itself rests on a horizontal table as shown in the attached figure. Assuming all surfaces are frictionless, determine the force F that must be applied to M so that m remains in a fixed position relative to M (that is, m doesn't move on the incline).

$$\mbox{(a)} \quad (M + m)gtan \theta$$

$$\mbox{(b)} \quad (Mtan \theta + m)g$$

$$\mbox{(c)} \quad \frac{(M + m)g}{tan \theta}$$

$$\mbox{(d)} \quad (M + m)g sin \theta$$

$$\mbox{(e)} \quad (M + m)g cos \theta$$

I know the answer is (a). Just don't understand how to arrive there.

Homework Equations

The Attempt at a Solution

My reasoning:

If there was no force being exerted on the system, i.e. $$F = F_{net} = 0$$, the small mass would slide down the triangular block due to the force of gravity ($$mgsin \theta$$). So, it would be safe to assume that if the system was at constant speed then the block would still slide down. Thus, the system must be accelerating in order for the small block to stay at rest relative to M.

However, how would the small block not move? Along the incline, there is only the force of gravity acting on the small block or would the force exerted by M on m somehow counteract that?

 

[bjgawp]

Bump ...

 

[Moetasim]

The correct answer is (a). To arrive at this answer, we need to analyze the forces acting on the system. First, we have the force of gravity acting on both masses, with a magnitude of Mg for the larger mass and mg for the smaller mass. This force is directed downwards, towards the ground.

Next, we have the normal force exerted by the inclined plane on the larger mass. This force is perpendicular to the surface of the inclined plane and is equal in magnitude to the component of the weight of the larger mass that is perpendicular to the surface. This component can be found using trigonometry as Mgcos\theta.

Finally, we have the force F that is being applied to the larger mass. This force is directed horizontally and is necessary to keep the system in equilibrium, with the smaller mass remaining in a fixed position relative to the larger mass.

In order for the smaller mass to remain in a fixed position, the net force acting on it must be zero. This means that the force of gravity acting on it must be balanced by the normal force exerted by the larger mass and the force F. In other words, we have:

F = mg + Mgcos\theta

Substituting the value of Mg from the equation above, we get:

F = mg + (Mgtan\theta)cos\theta

Simplifying, we get:

F = (M + m)gtan\theta

Thus, the correct answer is (a).