physicsss
- 319
- 0
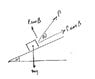
Knowing that the incline plane has an angle of 30 degrees and the coefficient of friction between a 60 lb block and the incline is 0.25, determine the smallest force P for which motion of the block up the incline is impending and the corresponding angle the force makes with the incline plane.
Is P= 0.25*cos(30)*60+sin(30)*60? But the book gives the answer of 41.7 while my answer is 42.99...any ideas?
Is P= 0.25*cos(30)*60+sin(30)*60? But the book gives the answer of 41.7 while my answer is 42.99...any ideas?