Incomplete transfer function for phase response

[kvtb]

Hi,

I'm currently busy with a 'small' project of translating an analog device (synthesizer, based on schematics) into a digital counterpart.
What I do is basically simulate the device using a SPICE model. Then I look at the outputs, and see if can fit some equation on it.

Based on the mathematical approximation of the circuit's behaviour, I implement an algorithm/DSP that shows the same behaviour as the analog version.
Now I've come to a small problem.

The circuit shows something that is a 2nd order active high pass filter. In my SPICE model, I did an AC simulation to get the frequency response of this filter (gain), and the phase response.

The next step was to find the transfer function for the filter. Well, that step already takes a week, so that's why this forum is my last resort, where I would like to show the problem. And hopefully someone has an answer.

Okay, the problem is as follows:
I use a standard transfer function for a 2nd order high pass filter:

H(s) = \frac{s^2}{s^2 + \omega_0/Q s + \omega_0^2}

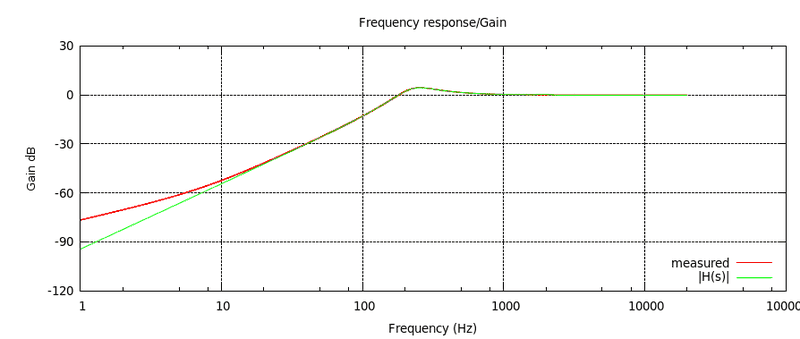
The following values give a perfect fit for the frequency response (ie gain, |H(s)|)
\omega_0 = 228.711
Q = 1.58195

look!

(freq_gain.png)

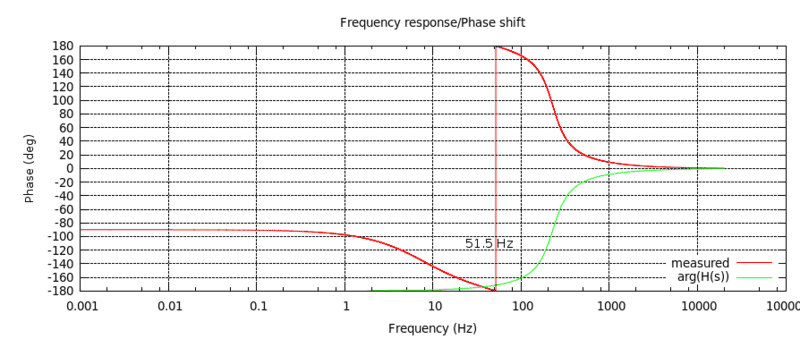
But when you look at the phase response, there is no fit at all:

(freq_phase.png)
(the phase jumps 360 degrees at 51.5 Hz)

So apparently, the transfer function is wrong or incomplete. Now my question is: how should the transfer function look like, to make sure both the measured frequency response and the measured phase response are perfectly captured in the equation?


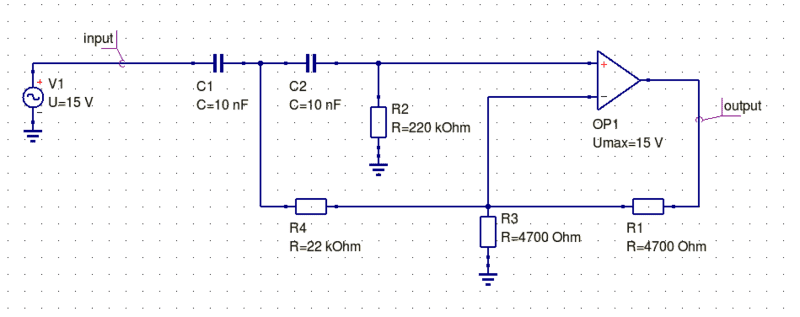
For your reference, here is the schematic that was simulated:

(hpf.png)

Thank you in advance for your help!

 

[berkeman]

Welcome to the PF. Why is R4 there?

 

[berkeman]

Welcome to the PF. Why is R4 there?

I guess maybe for the 2nd order transfer function? Can you link to the original circuit you are trying to simulate? (where did you get the original circuit?)

 

[kvtb]

Dear berkeman,
thanks for your reply,
the original circuit can be found here:
http://hardware.freepage.de/cgi-bin/feets/freepage_ext/339483x434877d/rewrite/raf909/rimshot.htm
or here:
http://www.kolumbus.fi/janne.husu/specs/909va.gif (in j9/j10)

 

[uart]

That phase doesn't jump! Phase angle wraps around (-180 = +180) and sometimes programs can't handle this wrapping correctly. That phase plot smoothly decreases from +270 to zero as frequency increases, that's all.

BTW. There is something else wrong with your plots. The green trace showing the phase of the stated transfer function should start at +180 and go to zero (not -180 to zero as shown).

 

[uart]

One final note.

If R4 were to have been connected to the output of the opamp (instead of the inverting input) then the circuit topology would have been precisely that of a second order high-pass "Sallen-Key" design. In this case you could just look up the transfer function of a Sallen Key filter and plug in the component values. As it is the circuit is a fair bit harder to analyse (but still do-able).

BTW. "Sallen-Key" was a very popular (and somewhat a standard) topology for active filters back in a their day.

 

[kvtb]

gentlemen,

your hints brought me back on the right track.

it could be a lucky shot, but found that a small change to the transfer function would give a perfect fit:

H(s) = \frac{s^2 + a s}{s^2 + \omega_0/Q s + \omega_0^2}

a new term has been added to the numerator: a s

The following values give a perfect fit for the frequency response and the phase response:
\omega_0 = 228.711
Q = 1.58195
a = -7.72458

see attached plots

Thanks

 

[uart]

Hi kvtb, quick question. What software are you using? I think it may be leading you astray as I question whether that phase response belongs to either that circuit or that transfer function.

Are you certain that the circuit diagram you posteed is the same one you're simulating?

 

[kvtb]

hello uart, I'm currently using qucs (http://qucs.sourceforge.net), but I'm considering re-simulating the same circuit in GNUcap just to be sure the software is not an issue here.

I indeed think that the circuit I'm simulating is the same I've posted here. Because just by looking at the theory (Sallen-Key like you mentioned) I expect a high pass filter, and the Bode-plot output of the AC simulation show a high pass filter


But yesterday I did a z-transform (manually) of the transfer function, then I implemented it, and I got a perfect.. low pass filter. So it's certain I made an error somewhere

 

[uart]

hello uart, I'm currently using qucs (http://qucs.sourceforge.net), but I'm considering re-simulating the same circuit in GNUcap just to be sure the software is not an issue here.

I indeed think that the circuit I'm simulating is the same I've posted here. Because just by looking at the theory (Sallen-Key like you mentioned) I expect a high pass filter, and the Bode-plot output of the AC simulation show a high pass filter


But yesterday I did a z-transform (manually) of the transfer function, then I implemented it, and I got a perfect.. low pass filter. So it's certain I made an error somewhere

Ok it mostly looks good. I still think that the "measured arg(H(s))" shown in green in your first post is the negative of what it should be, but the phase angle shown in red now looks good except for the "wrap around" issue.

You should read that phase as a continuous decreasing function, starting at -90 degrees and finishing at -360 degrees. Remember that in the context of steady state AC analysis that multiples of 360 degrees are meaningless, so you can just as well read that phase as going from +270 degrees down to 0 degrees.

BTW. It turns out that the circuit really is precisely a Sallen-Key HPF from Vin to the opamp input. I analysed it (by hand) and got the following transfer function.

\frac{v_+}{v_{in}} = \frac{s^2} {s^2 + \frac{2}{R_2 C} s + \frac{1}{R_2 R_4 c^2} }

What makes the circuit different is that the op-amp is no longer just a simple gain of two, because of the contribution of the current through R4 you get a whole another frequency response just from the opamp input to opamp output. I didn't analyse that part fully but I'm now confident that it does indeed introduce another zero, exactly as you had empirically deduced in your last post.

 

[uart]

Hang on. No there's still something bothering me about those results. I believe the results of the circuit simulation but I don't believe that the stated transfer fuction can give those phase results.

I can tell you for absolute certain that

H(s) = \frac{s^2 + a s}{s^2 + \omega_0/Q s + \omega_0^2}

will not give the phase response shown. There is abolutely no way that is going to give the 270 degrees phase shift as shown - just can't happen.

Edit : I take that back. I was thinking that "a" was a positive constant. I only just noticed that you stated that "a" is negaive. That totally changes things, when "a" is negative then it does indeed give the phase response as indicated.

 

[uart]

Still one thing that seems wrong. That circuit definitely has a gain of 2 (6dB) in the pass-band though the simulation shows zero dB. ?

 

[The Electrician]

I get a transfer function from V1 to opamp output of:

\frac{Vo}{V1} =(1+\frac{R_1}{R_3}) \frac{s^2-\frac{R_1R_3}{(R_1+R_3)R_2R_4C_2}s} {s^2 + (\frac{1}{R_2 C_2}+\frac{1}{R_2C_1}) s + \frac{1}{R_2 R_4 C_1C_2} }

This circuit is a little unusual in that the right end of R4 is connected to the minus input of the opamp, rather than to the output of the opamp.

I've attached two plots. The first shows the gain response of the given circuit in blue, and also the gain response if the right end of R4 were connected to the opamp output.

The second plot shows the corresponding phase responses.

 

[uart]

Yes I also analysed the TF from op-amp input to op-amp out last night to complete the overall response and got exactly the same answers as you "The Electrician". Good work. :)

I got :

\frac{v_{out}}{v_{in}} = \frac{2s (s - \frac{R}{2 R_2 R_4 C})} {s^2 + \frac{2}{R_2 C} s + \frac{1}{R_2 R_4 C^2} }

Where R is R_1 = R_3 and C is C_1 = C_2.

The right half plane zero means it's not a "mininum phase" system. The numerator phase runs from +270 degress back to +180 degree (rather than from +90 through to +180 as it would in a minumum phase system).

BTW The Electrician, do you have software to analyse the circuit or did you also analyse by hand. Just wondering as it seems like a dying art. I was starting to think that I'm the only one left alive that can still do stuff like that. ;)

 

[The Electrician]

BTW The Electrician, do you have software to analyse the circuit or did you also analyse by hand. Just wondering as it seems like a dying art. I was starting to think that I'm the only one left alive that can still do stuff like that. ;)

I use a method involving admittance matrices.

I explain it in this thread:

http://forum.allaboutcircuits.com/showthread.php?t=26710

 

[kvtb]

@uart and The Electrician. As a non-EE I'm quite impressed by your analysis of the schematics.

I'll try to perform a manual z-tranform based on the transfer functions you've supplied.
Thank you.