Waxbear
- 42
- 0
Homework Statement
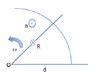
A light bulb with resistance R is attached on a metal rod which is rotating around the point O on the figure. The metal rod is in contact with an electrical conductor which is a part of a circle with radius d. The metal rod and the circular electrical conductor is a closed circuit. The rod now rotates with angular velocity \omega through the constant magnetic field pointing out from the paper.
a)
Find an expression for the induced current through the light bulb, expressed in terms of \omega, d, B and R.
Homework Equations
IR=vBr
where v is the tangential speed of the rod perpendicular to the B-field (every speed is perpendicular to the B-field, since we are looking at a plane) and r is the length of the rod moving at this speed.
I=\frac{\omega Br^{2}}{R}
v substituted for \omega r
The Attempt at a Solution
Since the every part of the rod is moving with different linear speeds, we should integrate the RHS from the 0 to d with respect to r and that should be it right?
i get:
I=\int^{d}_{0}\frac{\omega Br^{2}}{R}
I=\frac{d^{3}B\omega}{3R}
But when i look up the solution it says:
I=\frac{Bd^{2}\omega}{2R}
so who's right?
Edit: Problem solved!
Attachments
Last edited: