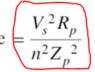Stu80 said:
I don't understand the question fully, what would be my starting expression? Pin (phase) = 3 V I cos∅?
i agree it isn't clearly stated .
How do I relate this to being proportional to torque?
i don't think you have to prove that because they already told you "
the expression for power input per phase (whatever that is
-jh)
is (∝ torque) "
I presume in the expression for the power input to the motor/phase that the resistance and impedance is that of the phase with them being denoted with a p?
i think that's safe to assume.
what else do we know?
We know that a motor has resistance and inductance
so we might express the impedance Z of a phase as R +jX
L.
And do we know that apparent power = V
2/Z ? If not, check that out with Ohm's Law.
And do we know that R/Z = cosine Φ ? If not, check that out with Pythagoras.
Hmmm. Might that awful looking fraction break down into something less fearsome?
Break it into a product of individual terms and see if anything logical falls out...
##\frac{1} {n}## X ## \frac {1}{n}## X V X ## \frac {V} {Z} ## X ## \frac {R} {Z}##now ignore the 1/n 's for a moment and concentrate on what's left
does it resemble VIcosΦ ?
Now what to do with those n's ?
I've atempted a number of solutions by substituting I and cos∅ for V/Z and R/Z respectively into Pin (phase) = 3 V I cos∅ but I don't come out with anything relevant.
why the 3 ?
Grad students who write the homework problems for textbook authors often leave clues for you to decipher just like in a mystery novel.
Always take a close look at what they give you and ask "Why did he say that " ?
And, take just one thought step at a time.
.
Here in homework forums we're not supposed to give you the answer, instead to lead your thoughts toward it.
To that end i just went back to very basics .
Basics rock ... Trust them !
old jim
"Never trust a computer with anything important."