You did a good job while I was sleeping, congratulation! So you assumed a superconducting coil driven with an ideal source.
Having a closed loop of superconducting wire, and keeping it at appropriate low temperature, and starting current in it by a magnet from outside - just pushing the electrons a bit- the current will flow -not really forever- but so long that we can say that it never stops.
In case of real materials, all currents decay if there is no source to keep it flowing. The free electrons of the conductor gain some velocity in the electric field built up by the source, but loose it when colliding with the ions of the conductor or with the other electrons. Their excess energy adds then to the thermal energy, it increases the average energy of the particles in the conductor, which means increasing temperature.
So you need to know that there is some loss in every circuit, and it can be represented by a resistor. This resistor is connected in series with the coil in your circuit.
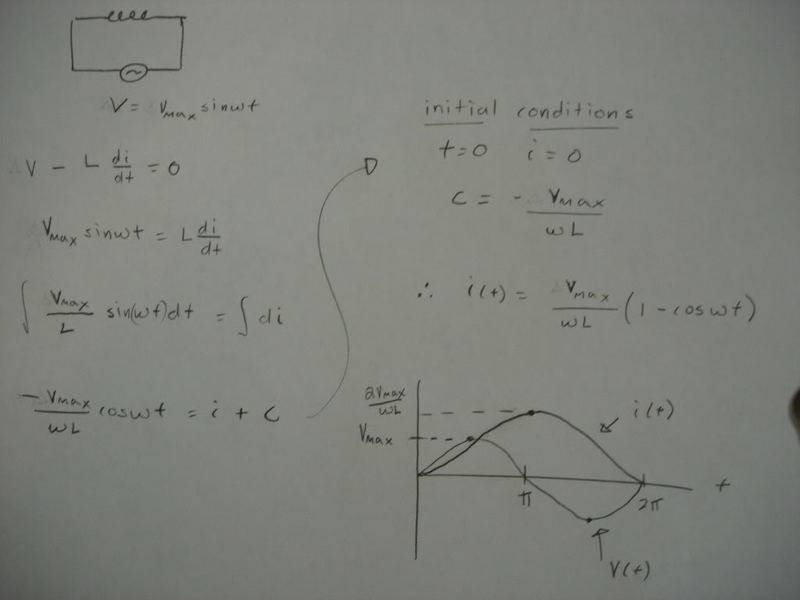
You have not run into this problem if you assumed that the generator voltage is Vmaxcos(ωt). This would mean a high current started by the generator at t=0, but this means an infinite dI/dt, that is a high counter-emf in the coil, which would allow zero current flowing initially, and a solution I=-Vmax/(ωL)sin(ωt).
Or even better, you could have used a current generator with current I=I(max)sin(ωt). Than the voltage across the inductor is simply VL=LdI/dt=Lωcos(ωt). No trouble with integration constant.
Now I outline the solution of the real case. I do not go into the details. You will learn them from Maths.
So you have an inductor L and a series resistor R and a source with emf Vmsin(ωt) (m means max).
The equation of the circuit is
L\frac{dI}{dt}+RI=V_m \sin(\omega t)
This is a first-order inhomogeneous differential equation, and the assigned homogeneous one is that with zero on the right-hand side:
L\frac{dI}{dt} +RI=0
General solution means such solution of a differential equation which can be fitted to arbitrary initial condition. You will learn that the general solution of a linear differential equation the general solution of the homogeneous equation + a particular solution of the original inhomogeneous one.
You will learn methods of solving differential equations. Now just accept that the general solution of L\frac{dI}{dt} +RI=0 is
I_h=A\exp(-\frac{R}{L}t)
where A is an arbitrary constant.
If you substitute it for I in the homogeneous equation you will see that it is really a solution.
The next step is to find a particular solution of the original inhomogeneous equation. One method is guessing the form of the function using free parameters which you choose so that the function satisfies the equation.
Try to find the particular solution Ip in the form
I_p=B\cos(\omega t) + C\sin(\omega t), and substitute back into the original equation.
L(-B\omega \sin(\omega t) + C\omega \cos(\omega t))+R(B\cos(\omega t) + C\sin(\omega t))=V_m \sin(\omega t)
Collect the cos(ωt) and sin(ωt) terms
(-BL\omega +CR-V_m)\sin(\omega t) + (CL \omega +RB)\cos(\omega t)=0
This equation is valid for any time t. That implies that the coefficients of both cos(ωt) and sin(ωt) are zero. (You can think that the equation is true for t=0. Then cos(ωt)=1 and sin(ωt)=0, so the coefficient of the cosine term has to vanish. In case if t=pi/(2ω), cos(ωt)=0 so the coefficient of the sine term has to vanish, too.) This results in two equations for the constants B and C.
-BL \omega +CR-V_m=0
CL \omega +RB=0
The solution is
B=-\frac{U_m L \omega}{L^2\omega^2+R^2}
C=\frac{U_m R }{L^2\omega^2+R^2}
So
I_p=-\frac{U_m L \omega}{L^2\omega^2+R^2}\sin(\omega t)+frac{U_m R }{L^2\omega^2+R^2}\cos(\omega t)
and the general solution is
I=A\exp{(-\frac{R}{L}t)}+B\cos(\omega t)+C\sin(\omega t)
You can fit A to the initial condition. You can choose I(0)=0, then A=-B, and
I=B(-\exp{(-\frac{R}{L}t)}+\cos(\omega t))+C\sin(\omega t)
Let's investigate this function: The exponential term will decay after some time, and the current will oscillate with the frequency of the generator forever with the "stationary" AC current
I=B\cos(\omega t)+C\sin(\omega t)=I _{max}sin(\omega t+\phi)
where Imax is the amplitude and φ is the phase with respect to the generator voltage.
I _{max}=\sqrt{B^2+A^2}=\frac{U_m}{\sqrt{L^2\omega^2+R^2}}
and
\phi=\arctan{B/C}=\arctan\frac{-L\omega}{R}
The voltage across the inductor is LdI/dT,
U_L=I_{max}\omega cos (\omega t+\phi)=I _{max}\omega sin (\omega t+\phi+\pi/2)
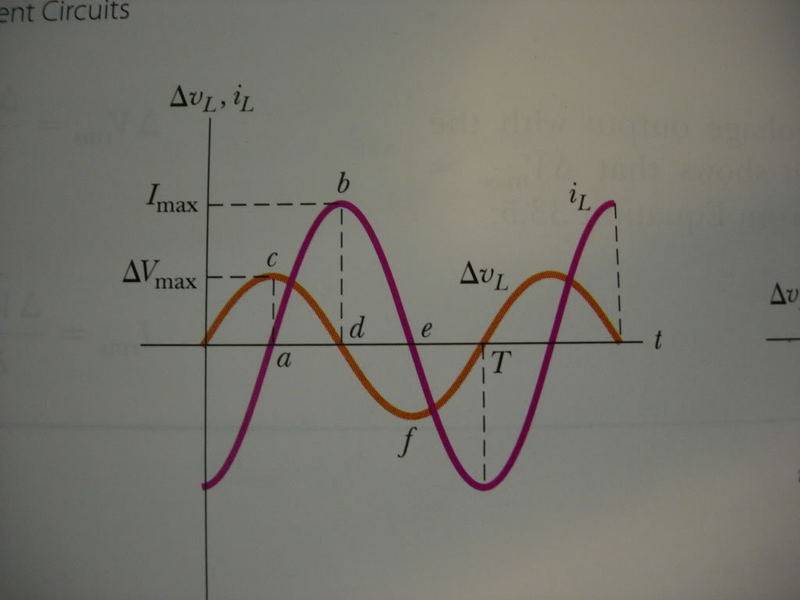
the voltage across the inductor leads he current by pi/2.
Consider the almost lossless case: R<<ωL. Then
I_{max}=\frac{U_m }{L\omega}
and
\phi=-\pi/2
The current lags the generator voltage by pi/2.
ehild