Saendy
- 2
- 0
Two objects of mass M (= 1 kg) each travel with identical speed (|v1| = |v2| = 3 m/s) making an angle of θ relative to the x-axis. After they collide with each other, they travel as one object of mass 2M and with a velocity v3 (|v3| = 2 m/s) in the horizontal direction.
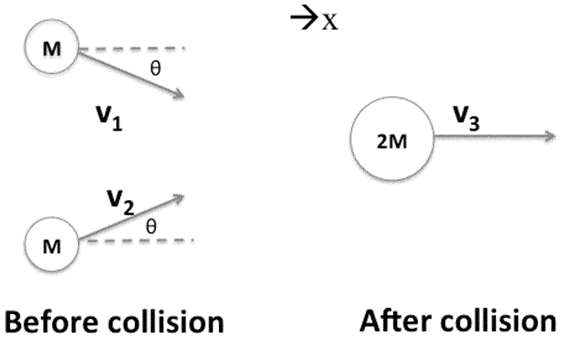
What is the value for angle θ in radians?
I tried m1 * v1 * cos(θ) + m2 * v2 * cos(θ) = mf * vf, but that was just a blind attempt to try something.
It's a practice exam question so I know the answer, but I want to know how to get there.
What is the value for angle θ in radians?
I tried m1 * v1 * cos(θ) + m2 * v2 * cos(θ) = mf * vf, but that was just a blind attempt to try something.
It's a practice exam question so I know the answer, but I want to know how to get there.