Now that you've solved the problem, I'll add my comment which I was afraid was too much of a hint, and then show how much simpler the math becomes.
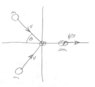
Symmetries often make problems in physics easier. You chose the x-axis to be the direction of one of the initial objects, but a more convenient choice would have been, as
@haruspex said, to choose the final momentum as the x-axis. That eliminates the need for the angle ##\phi##.
But what is that direction? By a symmetry argument, it has to be exactly halfway between the two identical velocity vectors. It can't be more toward one vector than the other, because there is nothing to distinguish those two directions. If you thought it was 10 degrees above the halfway point, why not 10 degrees below?
You can also prove that to yourself by doing the geometry for the vector addition, say by the parallelogram method.
Once you choose that halfway point as an x-axis, you realize that each original vector makes an angle of ##\theta/2## with the x-axis, the y-components of the original vectors cancel out, and the sum of the original x components of momentum is ##2mv \cos(\theta/2) = 2m \cdot v/3## so ##\cos(\theta/2) = 1/3##.