- #1
Quentin_C
- 19
- 0
Hi I am having trouble understanding how Bernoulli’s pressure gradients develop
I know the equation in a steady flow state (after the developed state ‘flushes’ thru) but I want to understand what mechanism lowers the pressure and increases the speed as the flow develops
The continuity principles tells us that this all must happen instantaneously
Here is my example
A funny shaped log is floating just submerged down a river flowing at 1 ms matching the current
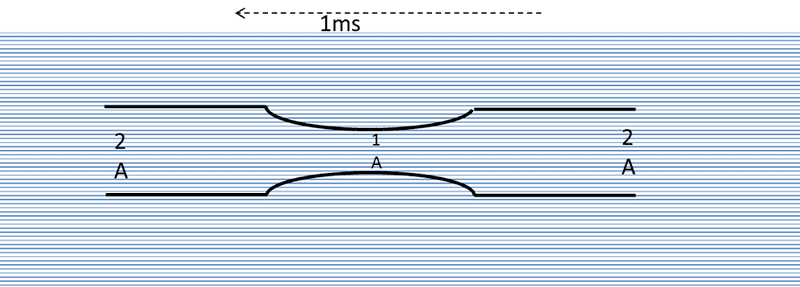
All of a sudden the rock very suddenly snags and stops it dead (with new velocity of 0ms) - the river continues to flow at 1ms
As I see it nothing has occurred to the internal fluid so this still travel at the same speed at equal pressure
 But I know that it doesn’t but how?
But I know that it doesn’t but how?
Attempt at a Solution Conservation of Mass
For volume of water (1ms *2A) to enter the pipe - the corresponding amount of water has to exit the pipe (1ms *2A) therefore for our control volume to balance we must have 2ms*1A in the constriction –
 Somehow the constriction has increased in speed
Somehow the constriction has increased in speed
 This means at that instant the fluid entering the pipe is traveling at 1ms and the fluid exiting the pipe is flowing at at 1ms but what mechanism that instant increases the speed in the constriction 1A and why ?
This means at that instant the fluid entering the pipe is traveling at 1ms and the fluid exiting the pipe is flowing at at 1ms but what mechanism that instant increases the speed in the constriction 1A and why ?
Work - the fluid in the constriction is experiencing no work it is being accelerated by the fluid entering the constriction as much as it is being decelerated by the fluid in front
Constant Energy Density
This must mean that’s the pressure at 1A must drop where as in the instant before this happens it is traveling at 1ms and the pressure is equal to the rest of the stream
 Becomes
Becomes
 Somehow the pressure that has decreasedInstantaneously there is no reason for this to happen, as no work has occurred Deceleration in fron =Acceleration behindPressure gradient – in the instant before the fluid did not have a pressure gradient in front or behind it was all equal and equal to the free stream so it did not accelerate down a gradientHow do the Bernoulli conditions develop instantaneously as conservation tells us they should ?
Somehow the pressure that has decreasedInstantaneously there is no reason for this to happen, as no work has occurred Deceleration in fron =Acceleration behindPressure gradient – in the instant before the fluid did not have a pressure gradient in front or behind it was all equal and equal to the free stream so it did not accelerate down a gradientHow do the Bernoulli conditions develop instantaneously as conservation tells us they should ?
I know the equation in a steady flow state (after the developed state ‘flushes’ thru) but I want to understand what mechanism lowers the pressure and increases the speed as the flow develops
The continuity principles tells us that this all must happen instantaneously
Here is my example
A funny shaped log is floating just submerged down a river flowing at 1 ms matching the current
All of a sudden the rock very suddenly snags and stops it dead (with new velocity of 0ms) - the river continues to flow at 1ms
As I see it nothing has occurred to the internal fluid so this still travel at the same speed at equal pressure
Attempt at a Solution Conservation of Mass
For volume of water (1ms *2A) to enter the pipe - the corresponding amount of water has to exit the pipe (1ms *2A) therefore for our control volume to balance we must have 2ms*1A in the constriction –
Work - the fluid in the constriction is experiencing no work it is being accelerated by the fluid entering the constriction as much as it is being decelerated by the fluid in front
Constant Energy Density
This must mean that’s the pressure at 1A must drop where as in the instant before this happens it is traveling at 1ms and the pressure is equal to the rest of the stream

