Integral Formulas for Center of Mass of Uniform Density

AI Thread Summary
The discussion focuses on calculating the center of mass for uniformly dense objects using integral formulas. The textbook suggests using the formula 1/V ∫ x dV, which is confusing for those unfamiliar with multiple variable integrals. A participant proposes an alternative approach for flat objects of uniform thickness by expressing dV as y(x) H dx, allowing the use of single-variable integrals. This method simplifies the problem for students not yet versed in multivariable calculus. The conversation highlights the need for accessible techniques in understanding center of mass calculations.
1MileCrash
Messages
1,338
Reaction score
41

Homework Statement



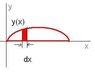
I'm being given problems regarding the center of mass of a uniformly dense object, and I am told by the textbook to use:

\frac{1}{V}\int x dV

I have no idea what to do with that. I'm pretty sure I won't be learning anything about multiple variable integrals for two years. There must be some other way?

Homework Equations





The Attempt at a Solution

 
Physics news on Phys.org
In case of a "flat" object of uniform thickness H, dV=y(x) H dx. So you need single-variable integrals.

ehild
 

Attachments

  • cm.JPG
    cm.JPG
    3.9 KB · Views: 419

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Confusion on product rule for mass of differential volume element
Replies
4
Views
2K
Finding Ctr of Mass of object w/ given uniform mass density
Replies
8
Views
2K
Calculate the center of mass of a non-uniform metal rod
Replies
13
Views
2K
Does Uniform Gravity Equate the Center of Mass with the Center of Gravity?
Replies
2
Views
1K
Electric field at a point inside a non-uniformly charged sphere
Replies
6
Views
1K
Center of mass of a disk with a hole
Replies
8
Views
4K
Center of mass of a sphere with cavity removed
Replies
4
Views
7K
Hole though the Earth and SHM: why is uniform density assumed?
Replies
7
Views
2K
Conservation of momentum (center of mass) in projectile launches
Replies
15
Views
1K
Help Me Solve My Diagram Problem: Calculating Center of Mass
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top