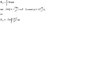Starproj
- 18
- 0
Hi,
I am studying a section on mass flux and have come across the following integral over an arbitrary surface. I am told that the integral equals 4pi radians. Can someone direct me to a proof of this and explain why the denominator (r2) drops out?
Thanks!
I am studying a section on mass flux and have come across the following integral over an arbitrary surface. I am told that the integral equals 4pi radians. Can someone direct me to a proof of this and explain why the denominator (r2) drops out?
Thanks!