- #1
Jurgen M
- Homework Statement
- I have problem to solve this tasks.
- Relevant Equations
- Calculus, infinity
Are both integral on picture below equal zero?
I think both are zero, area of zero section under function must be zero.
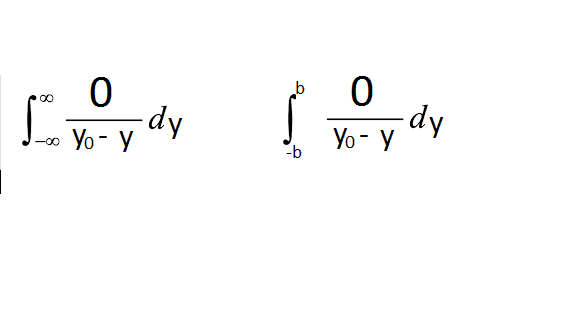
If M=∞, b=∞ , what is reslut?
Logically ∞/∞ will be 1..but...
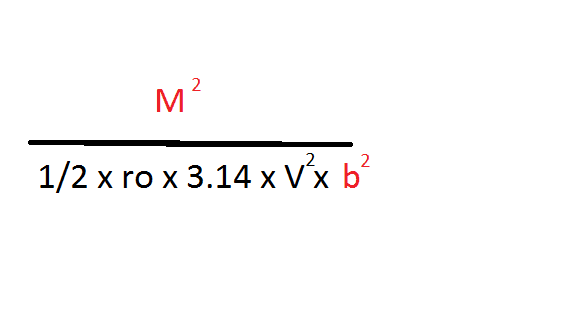
I think both are zero, area of zero section under function must be zero.
If M=∞, b=∞ , what is reslut?
Logically ∞/∞ will be 1..but...