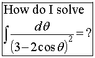Integrating Rational Functions: How to Solve Challenging Integrals?

[bomba923]

How do I solve this integral?? (it's in the attachment)
(my-efforts.gif just explains a failed attempt)

 

[dextercioby]

I've struggled with it and i couldn't come up with an answer.All i can tell u is that it cannot be factorized (decomposed in simple fractions) because it's not rational.The square in the denominator is the most annoying...

Daniel.

 

[bomba923]

Wait..sorry neverm0nd----i found a solution!

Just use the Heaviside Method and make A, B, C--

substitute x= cos (theta)
and that dx= -sin (theta)
and then divide by the -sin (theta) as -(1-x^2)
-----------------------------
put A/((3-2x)^2)+B/((1+x)^(1/2))+C/((1-x)^(1/2),
then solve using heaviside

 

[dextercioby]

I told u it doesn't work...
\int \frac{d\theta}{(3-2\cos\theta)^{2}}
,via the substitution
\cos\theta\rightarrow x
becomes
-\int \frac{dx}{\sqrt{1-x^{2}}(3-2x)^{2}}
which is very irrational.

So your
\frac{A}{(3-2x)^{2}}+\frac{B}{\sqrt{1-x}}+\frac{C}{\sqrt{1+x}}
doesn't lead anywhere.

Daniel.

 

[Inquisitive_Mind]

Use t method? (i.e. set t=tan(x/2), such that cos(x)=(1-t^2)/(1+t^2))

 

[marlon]

Use t method? (i.e. set t=tan(x/2), such that cos(x)=(1-t^2)/(1+t^2))

This is the right way. I got to a solution like this. Besides the new differential shall be 2dt/(1+t²). Then you can manipulate this integral so that you will get two integrals. One of them is elementary (arcustangens)and the other one can be soved with partial integration...


Just try it...

remember with manipulation i mean something like this \frac {1+t^2}{(1+5t^2)^2} = \frac{1+ 5t^2}{(1+5t^2)^2} + \frac{-4t^2}{(1+5t^2)^2}


marlon

 

[marlon]

I told u it doesn't work...
\int \frac{d\theta}{(3-2\cos\theta)^{2}}
,via the substitution
\cos\theta\rightarrow x
becomes
-\int \frac{dx}{\sqrt{1-x^{2}}(3-2x)^{2}}
which is very irrational.

So your
\frac{A}{(3-2x)^{2}}+\frac{B}{\sqrt{1-x}}+\frac{C}{\sqrt{1+x}}
doesn't lead anywhere.

Daniel.

And besides this decomposition is even wrong. You did not apply the rules correctly...But drop it because it is useless here and certainly with the sqrt you CANNOT do this !

marlon

 

[dextercioby]

I knew the decomposition was wrong,i told him that substitution would lead nowhere.
Anyways,my result is
\int \frac{d\theta}{(3-2\cos\theta)^{2}}=\frac{4}{5}\frac{\tan\frac{\theta}{2}}{1+5\tan^{2}\frac{\theta}{2}}+\frac{6\sqrt{5}}{25}\arctan(\sqrt{5}\tan\frac{\theta}{2})+C

Daniel.

 

[marlon]

I knew the decomposition was wrong,i told him that substitution would lead nowhere.
Anyways,my result is
\int \frac{d\theta}{(3-2\cos\theta)^{2}}=\frac{4}{5}\frac{\tan\frac{\theta}{2}}{1+5\tan^{2}\frac{\theta}{2}}+\frac{6\sqrt{5}}{25}\arctan(\sqrt{5}\tan\frac{\theta}{2})+C

Daniel.

You see, my trick worked...

marlon

 

[bomba923]

Does the partial fractions technique work only for rational functions?
But yeah, my decomposition was wrong (now i see!)

 

[HallsofIvy]

Since only rational functions are fractions, yes, partial fractions only works for rational functions!