Integration by parts of a differential

[maistral]

I'll cut the long story short. What on Earth happened here:

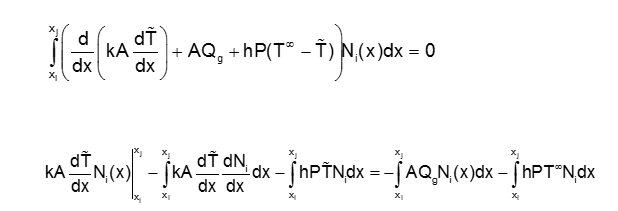
I seem to be unable to do the integration by parts of the first term. I end up with a lot of dx's.

 

[Mark44]

Try splitting the integral into two parts, with this as the first one:
$\int_{x_i}^{x_j} \frac d{dx}\left( kA\frac{dT}{dx}\right)N_i(x)dx$

 

[maistral]

I do know how to split the integral. I just wonder what happened to the identity. Judging from the result, as in the format int(u dv) = uv - int(v du);
u = d/dx (kA dT/dx)
dv = N_i(x)dx

The problem maybe is that I don't know how to calculate du. What would be the result?

 

[Daniel Gallimore]

I do know how to split the integral. I just wonder what happened to the identity. Judging from the result, as in the format int(u dv) = uv - int(v du);
u = d/dx (kA dT/dx)
dv = N_i(x)dx

The problem maybe is that I don't know how to calculate du. What would be the result?

Because we're working with nice single-variable functions (presumably), $$dq=\frac{dq}{dx} \, dx=\frac{d}{dx}(q) \, dx$$ To me, it looks like they let $$dv=\frac{d}{dx}\left(kA \frac{dT}{dx}\right) \, dx$$ and $$u=N_i(x)$$ This would imply $$v=kA \frac{dT}{dx}$$ and $$du=dN_i=\frac{dN_i}{dx} \, dx$$ which appears to be consistent with the result they got.

 

[Mark44]

I do know how to split the integral. I just wonder what happened to the identity. Judging from the result, as in the format int(u dv) = uv - int(v du);
u = d/dx (kA dT/dx)
dv = N_i(x)dx

The problem maybe is that I don't know how to calculate du. What would be the result?

What happens if you instead let $u = N_i(x)$ and $dv = \frac d {dx} \left(kA \frac{dT}{dx}\right) dx$? Finding v shouldn't be that difficult.

 

[maistral]

Thanks!