AlonsoMcLaren
- 89
- 2
Homework Statement
Integrate \int_{-\infty}^{\infty} dx \ x^{-3}(sin x -x )
Homework Equations
Residual theorem, Jordan's lemma
The Attempt at a Solution
\int_{-\infty}^{\infty} dx \ x^{-3}(sin x -x )<br /> <br /> = I am \ (PV\int_{-\infty}^{\infty} dx \ x^{-3}(e^{ix} -ix ))
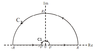
In the contour, if we let R goes to infinity and ρ goes to zero, then we have
\oint_{Total}^{ } dz \ z^{-3}(e^{iz} -iz) = \int_{C_{1}}^{ } dz \ z^{-3}(e^{iz} -iz) + \int_{C_{2}}^{ } dz \ z^{-3}(e^{iz} -iz) + PV \int_{-\infty}^{\infty} dx \ x^{-3}(e^{ix} -ix)
Because the only singularity is 0, not inside the contour. By residual theorem (or Cauchy's theorem),
\oint_{Total}^{ } dz \ z^{-3}(e^{iz} -iz) = 0
By Jordan's lemma, as R goes to infinity,
\int_{C_{2}}^{ } dz \ z^{-3}(e^{iz} -iz) =0
For the C1 contour
\int_{C_{1}}^{ } dz \ z^{-3}(e^{iz} -iz)= \int_{\pi}^{0 } d(\rho e^{i\theta }) \frac{e^{i\rho e^{i\theta }} -i\rho e^{i\theta }}{(\rho e^{i\theta })^{3}}= i \int_{\pi}^{0 }\frac{e^{i\rho e^{i\theta }}-i\rho e^{i\theta}}{\rho ^{2}e^{2i\theta }} d \theta
But as ρ goes to 0, \frac{e^{i\rho e^{i\theta }}-i\rho e^{i\theta}}{\rho ^{2}e^{2i\theta }}
goes to infinity. So I am stuck.
The final answer, according to WolframAlpha, is -π/2