killerfish
- 16
- 0
Hi,
i have a problem with integration a function with a unit step function.
Given,
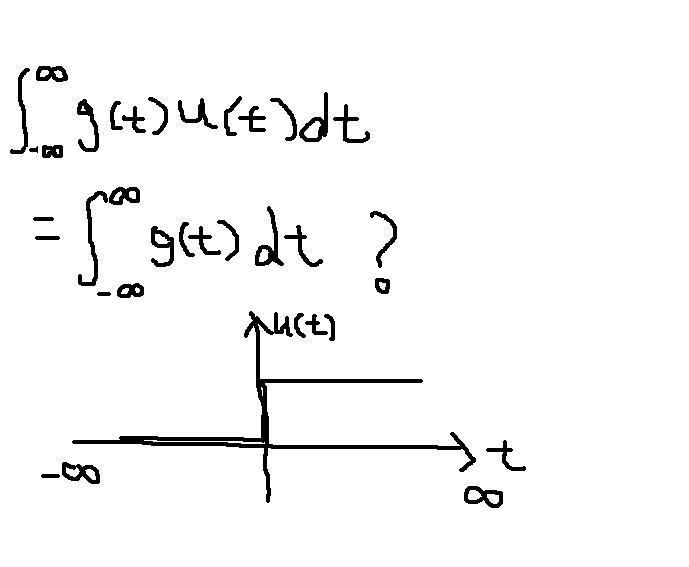
Refer to the image, i dun understand is that u(t) is equal to 1 from a definite integration from -\infty to \infty since u(t)=1 from -\infty to 0 and u(t)=0 from 0 to \infty.
Thanks.
i have a problem with integration a function with a unit step function.
Homework Statement
Given,
Refer to the image, i dun understand is that u(t) is equal to 1 from a definite integration from -\infty to \infty since u(t)=1 from -\infty to 0 and u(t)=0 from 0 to \infty.
Thanks.